"2차원 쌍곡기하학의 테셀레이션"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 44번째 줄: | 44번째 줄: | ||
==관련된 항목들== | ==관련된 항목들== | ||
* [[Fundamental domain의 면적에 대한 지겔의 정리]] | * [[Fundamental domain의 면적에 대한 지겔의 정리]] | ||
| − | + | * [[클라인의 4차곡선]] | |
| + | * [[컴팩트 리만곡면의 자기동형군에 대한 Hurwitz 정리]] | ||
2013년 6월 8일 (토) 09:18 판
개요
- 공간을 똑같이 생긴 삼각형으로 채운 그림에는 위상수학, 미분기하학, 군론 등등 많은 수학이 들어 있다
쌍곡기하학의 삼각형의 넓이
사람들은 유클리드 기하학이 가장 쉬운 기하학이라고 생각을 하지만, 삼각형의 넓이 구하는 일을 생각하면 꼭 그렇지가 않다. 초등학교에 가면 삼각형의 넓이 구하는 방법을 가르쳐주는데, 변의 길이를 적어도 하나는 꼭 알아야 한다. 그런데 쌍곡기하학에서는 변의 길이를 알 필요가 전혀 없다. 각도가 모든 것을 결정한다!!! 삼각형의 세 각이 \(\alpha, \beta, \gamma\)로 주어져 있다면 그 넓이는 \(\pi - \alpha- \beta- \gamma\) 가 된다.
(2,3,7)-삼각형을 이용한 테셀레이션
(2,3,7)-삼각형
- (2,3,7)이란 삼각형의 세 각이 각각 \(\frac{\pi}{7},\frac{\pi}{3},\frac{\pi}{2}\) 임을 의미
- 이 세각의 크기를 모두 더하면, 180도보다 작게 됨을 확인할 수 있다
\[\frac{\pi}{7}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{41\pi}{42}\]
- 쌍곡기하학에서의 곡률은 음수이기 때문에 나타나는 현상이다
- 단위원판을 겹치지 않으면서도 빽빽하게 채울수 있는 가장 작은 삼각형
- \(1- (\frac{1}{l}+\frac{1}{m}+\frac{1}{n})\)를 0보다 크면서 동시에 가장 작게 만드는 자연수 l,m,n 를 찾는 것과 같게 된다.
- 그림에 있는 삼각형 한 조각을 들고 와서 각을 잰다. 그러기 위해서는 각을 재려는 점 주변에 삼각형이 몇개 있는지 세서 나누면 된다. 각각 4조각, 6조각, 14조각이 있다. 그러므로 각도는 \[\frac{\pi}{7},\frac{\pi}{3},\frac{\pi}{2}\]로 주어진다.
- 위의 넓이 공식에 의하면, 이 삼각형의 넓이는 \[\pi-\frac{\pi}{7}-\frac{\pi}{3}-\frac{\pi}{2}=\frac{\pi}{42}\]
$(2,3,\infty)$-삼각형
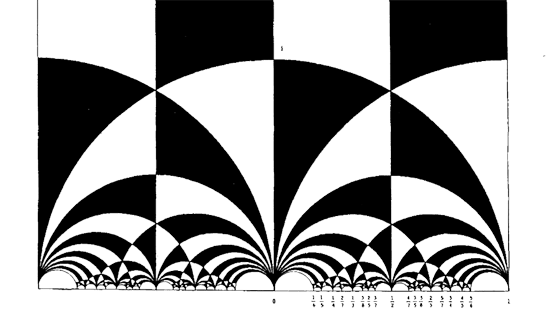
- 가령 아래 그림 역시 쌍곡기하학의 그림인데, 모듈라 군(modular group)이라고 하는 수학적으로 매우 중요한 대상을 공부할 때, 반드시 등장한다. 참고로 이 그림에 등장하는 삼각형은 \( (2, 3, \infty)\)이다.
- 이는 푸앵카레 상반평면 모델에서의 테셀레이션이다
반전사상
- 반전 사상(inversion)은 푸앵카레 unit disk 모델에서, 모든 점들의 길이를 보존하는 등거리사상
- 따라서 아래의 그림에 있는 삼각형들은 쌍곡기하학의 관점에서 보면, 모두 그 크기와 모양이 똑같음.
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://docs.google.com/file/d/0B8XXo8Tve1cxTTNiWEVhdXpHdlE/edit
- 코드 해설은 Complex analysis with Mathematica, Chapter 22. 참조