의구 (Pseudosphere)

개요

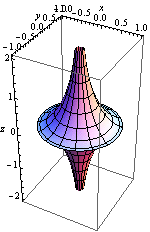
• 음의 상수곡률곡면들을 칭하는 말
• 쌍곡기하학 의 발전에서 중요한 역할

• http://www.math.colostate.edu/~croke/math/summerGeom/documents/pseudosphere.pdf

tractroid

• 추적선 (tractrix)의 회전으로 얻어지는 곡면

• 매개화\[\mathbf{x}(u,v)=(\cos (u) \text{sech}(v),\sin (u) \text{sech}(v),v-\tanh (v))\]

제1기본형식과 크리스토펠 기호

• \(E=\text{sech}^2(v)\), \(F=0\),\(G=\tanh ^2(v)\)
• 크리스토펠 기호\[\begin{array}{ll} \Gamma _{11}^1 & 0 \\ \Gamma _{12}^1 & -\tanh (v) \\ \Gamma _{21}^1 & -\tanh (v) \\ \Gamma _{22}^1 & 0 \\ \Gamma _{11}^2 & \text{csch}(v) \text{sech}(v) \\ \Gamma _{12}^2 & 0 \\ \Gamma _{21}^2 & 0 \\ \Gamma _{22}^2 & \text{csch}(v) \text{sech}(v) \end{array}\]

역사

• 1829 - 볼리아이, 가우스, 로바체프스키가 쌍곡기하학을 발견
• 1868 - 벨트라미에 의해 '의구(pseudosferiche)'라는 이름이 붙여짐
• 수학사 연표

메모

• http://xahlee.org/surface/pseudosphere/pseudosphere.html
• http://www.math.colostate.edu/~croke/math/summerGeom/
• http://danielwalsh.tumblr.com/day/2010/12/11

관련된 항목들

• 상수곡률곡면과 사인-고든 방정식
• 쌍곡기하학

매스매티카 파일 및 계산 리소스

• https://docs.google.com/leaf?id=0B8XXo8Tve1cxOTIxMGRhNzAtNmY1OS00NzRlLWFkYTQtMzE2ZjlmZWM5NDdh&sort=name&layout=list&num=50

수학용어번역

• Pseudo - 대한수학회 수학용어집
• pseudo-sphere 의구, 유사구면

사전 형태의 자료

• http://ko.wikipedia.org/wiki/
• http://en.wikipedia.org/wiki/Pseudosphere

리뷰, 에세이, 강의노트

• Claudio Bartocci Perrault's watch and Beltrami's pseudosphere: A story without a moral

관련논문

• Radeschi, Marco, and Burkhard Wilking. “On the Berger Conjecture for Manifolds All of Whose Geodesics Are Closed.” arXiv:1511.07852 [math], November 24, 2015. http://arxiv.org/abs/1511.07852.