타원 내의 격자점 개수 문제
Pythagoras0 (토론 | 기여)님의 2014년 5월 26일 (월) 22:24 판
개요
- 타원 \(Ax^2+Bxy+Cy^2=T\) , \(A>0\), \(C>0\), \(T>0\)
- 타원 내부의 넓이는 \(\frac{2\pi T}{\sqrt{|\Delta|}}\)
- \(\Delta=b^2-4ac\)
- 정리
타원 \(Ax^2+Bxy+Cy^2=T\) , \(A>0\), \(C>0\), \(T>0\) 의 내부에 있는 정수격자점의 개수 \(N(T)\)에 대하여, $T\to \infty$일 때, 다음이 성립한다. \[|N(T)-\frac{2\pi T}{\sqrt{|\Delta|}}| \approx O(\sqrt{T})\]
예
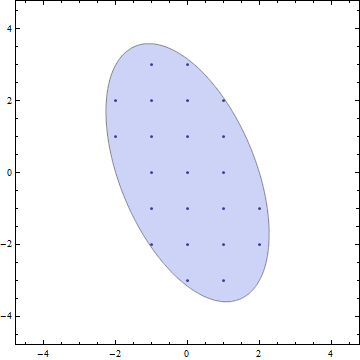
- 타원 $5 x^2+3 x y+2 y^2=20$ 의 경우
- 내부의 격자점의 개수는 23, 타원의 넓이는 $\frac{40 \pi }{\sqrt{31}}\sim 22.5699$
관련된 항목들