톨레미의 정리

개요

(정리)

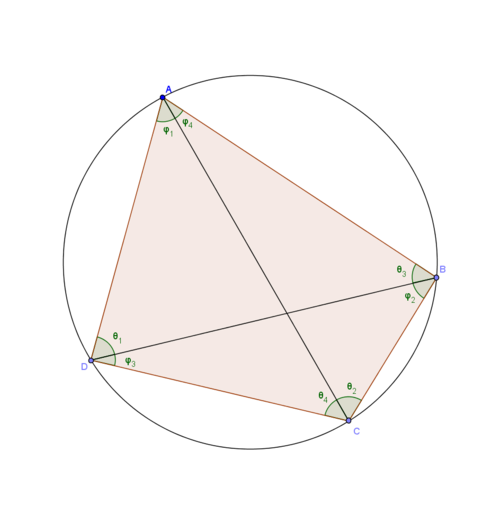
사각형이 원에 내접할때, 두 대각선의 길이의 곱은 서로 마주보고 있는 두 변의 쌍의 길이의 곱의 합과 같다.

\(\overline{AC}\cdot \overline{BD}=\overline{AB}\cdot \overline{CD}+\overline{BC}\cdot \overline{AD}\)

[/pages/3324857/attachments/3540037 PtolemyQD.jpg]

\(AC=\sin (\theta_1+\varphi_3) \)
\(BD=\sin (\varphi_1+\varphi_4)=\sin (\varphi_1+\varphi_3) \)
\(AB=\sin \theta_1 \)
\(CD=\sin \varphi_1 \)
\(BC=\sin \varphi_3 \)
\(AD=\sin \theta_3 \)
\(AC\cdot BD=\sin (\theta_1+\varphi_3) \sin (\varphi_1+\varphi_3) \)
\(AB\cdot CD+BC\cdot AD=\sin \theta_1\sin \varphi_1+\sin \varphi_3\sin \theta_3 \)
톨레미의 정리 \[\sin (\theta_1+\varphi_3) \sin (\varphi_1+\varphi_3)=\sin \theta_1\sin \varphi_1+\sin \varphi_3\sin \theta_3\]
\(\theta_1+\varphi_3=\pi/2\)이면,\(\theta_3+\varphi_2=\theta_3+\varphi_1=\pi/2\) 이다.
따라서 \(\sin (\theta_1+\varphi_3)=1,\sin \theta_1=\cos \varphi_3, \sin \theta_3=\cos \varphi_1 \)
톨레미의 정리로부터 다음을 얻는다\[\sin (\varphi_1+\varphi_3)= \sin \varphi_1\cos \varphi_3+\sin \varphi_3\cos \varphi_1\]
삼각함수의 덧셈과 곱셈 공식
http://www.cut-the-knot.org/proofs/sine_cosine.shtml