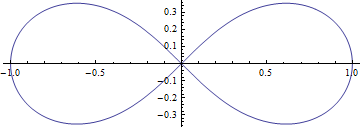
렘니스케이트(lemniscate) 곡선의 길이와 타원적분

개요

극좌표계에서 방정식 $r^2=\cos2\theta$ 로 주어진 곡선을 베르누이의 렘니스케이트 곡선이라 부름.
카테시안 좌표계에서는 $(x^2 + y^2)^2=x^2 - y^2$로 주어진다

렘니스케이트 곡선의 둘레의 길이와 타원적분

정리

렘니스케이트 곡선의 둘레의 길이 $L$은 타원적분으로 표현되며 다음이 성립한다 \[L=4\int_0^1\frac{dx}{\sqrt{1-x^4}}=2\sqrt{2}K(\frac{1}{\sqrt{2}})=5.2441\cdots\] 여기서 $K$는 제1종타원적분 K (complete elliptic integral of the first kind) $$K(k) = \int_0^{\frac{\pi}{2}} \frac{d\theta}{\sqrt{1-k^2 \sin^2\theta}}.$$ 또한 다음이 성립한다 \[L=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}}\] 여기서 $B$는 오일러 베타적분(베타함수)이고, $\Gamma$는 감마함수

증명

렘니스케이트 곡선은 $x=r(\theta)\cos\theta,y=r(\theta)\sin\theta$로 매개화되며, 다음을 확인할 수 있다 $$ r'(\theta)=-\frac{\sin 2\theta}{r(\theta)} $$ 매개화를 이용하여, 둘레의 길이를 계산하면 다음을 얻는다 \[L=4\int_{0}^{\pi/4}\sqrt{r'(\theta)^2+r(\theta)^2}\,d\theta=4\int_{0}^{\pi/4}\sqrt{\frac{\sin^2 2\theta}{r^2(\theta)}+r^2(\theta)}\,d\theta=4\int_{0}^{\pi/4}\frac{1}{\sqrt{\cos 2\theta}}\,d\theta\] 이 때, $\cos 2\theta=\cos^2{\phi}$ 를 이용하여 치환하면, \[d\theta=\frac{\sin\phi\cos\phi}{\sqrt{1-\cos^4\phi}}\,d\phi=\frac{\cos\phi}{\sqrt{1+\cos^2\phi}}\,d\phi,\] \[L=4\int_0^{\pi/2}\frac{1}{\sqrt{1+\cos^2 \phi}}\,d\phi=2\sqrt{2}\int_0^{\pi/2}\frac{1}{\sqrt{1-\frac{1}{2}\sin^2 \phi}}\,d\phi \label{eq1}\] \ref{eq1}로부터 다음을 얻는다 $$ L=2\sqrt{2}K(1/\sqrt{2}) $$ \ref{eq1}에서 $x=\cos\phi$로 치환하면, \[L=4\int_0^{\pi/2}\frac{1}{\sqrt{1+\cos^2 \phi}}\,d\phi=4\int_0^1\frac{dx}{\sqrt{1-x^4}}=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}}=5.2441\] ■

가우스의 렘니스케이트 상수

가우스의 렘니스케이트 상수 $\omega$를 다음과 같이 정의

\[\omega:=L/2=2.62\cdots\]

타원곡선 y²=x³-x의 주기(periods)이며 초월수임.

원주율과의 비교

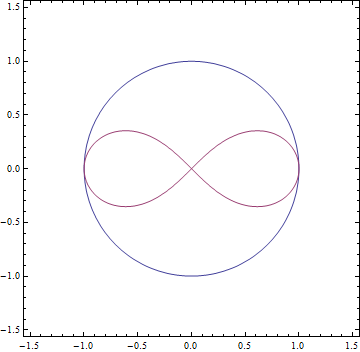
가우스는 단위원의 둘레의 길이와 렘니스케이트의 둘레의 길이의 비율을 계산하였다

\[\frac{\pi}{2}=\int_0^1\frac{dx}{\sqrt{1-x^2}}=1.57\cdots\] \[\frac{\omega}{2}=\int_0^1\frac{dx}{\sqrt{1-x^4}}=1.31\cdots\] \[\frac{\pi }{\omega}=1.1981402347\cdots\]

가우스는 이 수가 $\sqrt{2}$과 1의 산술 기하 평균 (arithmetic-geometric mean)이 되는 것을 관찰

정리

다음이 성립한다 \[\frac{\pi }{\omega}=M(1,\sqrt2)\] 여기서 $M(a,b)$ 은 두 수 $a, b$의 산술 기하 평균 (arithmetic-geometric mean)

증명

렘니스케이트 상수의 타원적분 표현 $$\frac{\omega}{2}=\frac{1}{\sqrt{2}}K(\frac{1}{\sqrt2})\label{ome}$$ 한편 란덴변환(Landen's transformation) 에서 다음을 얻었다 $$K(\frac{1}{\sqrt2})=\frac{\pi}{2M(1,\frac{1}{\sqrt2})}\label{landen}$$ \ref{ome}와 \ref{landen}를 이용하여 다음을 얻는다: $$\frac{\pi}{\omega}=\frac{2K(\frac{1}{\sqrt2}){M(1,\frac{1}{\sqrt2})}}{\sqrt{2}K(\frac{1}{\sqrt2})} = \sqrt{2}M(1,\frac{1}{\sqrt2})=M(1,\sqrt2)$$ ■

테이블

$$ \begin{array}{ccc} {n} & a_n & b_n \\ \hline 0 & 1.4142135623730950488 & 1.0000000000000000000 \\ 1 & 1.2071067811865475244 & 1.1892071150027210667 \\ 2 & 1.1981569480946342956 & 1.1981235214931201226 \\ 3 & 1.1981402347938772091 & 1.1981402346773072058 \\ 4 & 1.1981402347355922074 & 1.1981402347355922074 \\ 5 & 1.1981402347355922074 & 1.1981402347355922074 \\ 6 & 1.1981402347355922074 & 1.1981402347355922074 \\ 7 & 1.1981402347355922074 & 1.1981402347355922074 \\ 8 & 1.1981402347355922074 & 1.1981402347355922074 \\ 9 & 1.1981402347355922074 & 1.1981402347355922074 \\ \end{array} $$

재미있는 사실

곡선의 모양이 무한대 기호와 같음
무한대는 그 한계가 없기에 리본을 뜻하는 'lemniscus'라는 말로 불릴 때도 있었으며, 그로인해 무한대 기호가 누운 8자 모양이 되었다는 설이 있음

역사

1684 베르누이 'Acta Eruditorum'
18세기 Fagnano, Euler, and Legendre 에 의한 연구
1798~1799년의 시기에 가우스는 이 곡선의 길이와 관련하여 다음과 같은 기록을 일기에 남김. (Pi-unleashed, 99p)

We have gained some very elegant details about the lemniscate, which have exceeded all expectations, and indeed using methods which open up an entirely new field. That the AGM is equal to $\frac{\pi }{\omega}$ between 1 and $\sqrt{2}$ we have confirmed up to the 11th decimal digit; if this is proven, then a truly new field of analysis stands before us.

수학사 연표

수학용어번역

http://www.google.com/dictionary?langpair=en|ko&q=lemniscate
Latin lemniscus meaning "ribbon"
번역용어제안
- 쌍타원, 겹타원, 이중타원, 나비리본
- '베르누이의 연주형'(lemniscate) http://www.google.com/dictionary?langpair=ko|ko&q=연주
lemniscate - 대한수학회 수학용어집

매스매티카 파일 및 계산 리소스

사전 형태의 자료

리뷰, 에세이, 강의노트

From Lintearia to Lemniscate I : physics to mathematics R Sridharan
From Lintearia to Lemniscate II: Gauss and Landen’s Work R Sridharan
The Lemniscate and Fagnano's Contributions to Elliptic IntegralsRaymond Ayoub, Archive for History of Exact Sciences, 1984