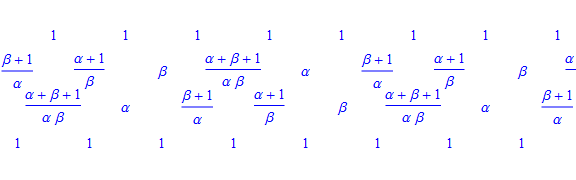"라이네스 차분방정식"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) (→관련논문) |
Pythagoras0 (토론 | 기여) |
||
| 29번째 줄: | 29번째 줄: | ||
* [[콕세터 프리즈]] | * [[콕세터 프리즈]] | ||
[[파일:콕세터 프리즈4.png]] | [[파일:콕세터 프리즈4.png]] | ||
| + | ===$A=0$=== | ||
| + | * 다음과 같은 주기 6인 수열을 얻는다 | ||
| + | $$ | ||
| + | \alpha ,\beta ,\frac{\beta }{\alpha },\frac{1}{\alpha },\frac{1}{\beta },\frac{\alpha }{\beta },\alpha ,\beta ,\cdots | ||
| + | $$ | ||
| 34번째 줄: | 39번째 줄: | ||
* [[Pentagramma Mirificum]] | * [[Pentagramma Mirificum]] | ||
* http://www.jstor.org/stable/2324138 | * http://www.jstor.org/stable/2324138 | ||
| + | * We show that if $A \not= 1 $ then f is a twist map, with rotation numbers tending to 1/5 as the curves tend to infinity. Beukers and Cushman have shown that the rotation numbers are monotonic increasing if $A < 1,$ and decreasing if $A \gt 1.$ Using number theory we classify the periods of periodic orbits. | ||
| 44번째 줄: | 50번째 줄: | ||
==매스매티카 파일 및 계산 리소스== | ==매스매티카 파일 및 계산 리소스== | ||
* https://docs.google.com/file/d/0B8XXo8Tve1cxN3RUaHRNY3NrQkk/edit?usp=drivesdk | * https://docs.google.com/file/d/0B8XXo8Tve1cxN3RUaHRNY3NrQkk/edit?usp=drivesdk | ||
| + | |||
| + | |||
| + | |||
| + | ==리뷰, 에세이, 강의노트== | ||
| + | * [http://zakuski.utsa.edu/~gokhman/ecz/gu.html Geometric Unfolding of a Difference Equation] E. Christopher Zeeman, K.B., F.R.S. UT San Antonio, March 10, 1997 / Trinity University, March 17, 1997 | ||
2013년 11월 1일 (금) 11:38 판
개요
- 복소수 $A\in \mathbb{C}$에 대하여, 다음의 점화식을 Lyness 차분방정식이라 부른다
$$ x_{n+1}=\frac{A+x_{n}}{x_{n-1}} \label{lyn} $$
- $x_0=\alpha,x_1=\beta$와, 점화식 \ref{lyn}에 의해 다음과 같은 수열 $\{x_n\}_{n\geq 0}$을 얻는다
$$ \alpha ,\beta ,\frac{A+\beta }{\alpha },\frac{A+A \alpha +\beta }{\alpha \beta },\frac{A+A \alpha +\beta +A \alpha \beta }{A \beta +\beta ^2},\frac{\alpha \left(\beta +A \left(1+\alpha +(A+\alpha ) \beta +\beta ^2\right)\right)}{(A+\beta ) (A+A \alpha +\beta )},\cdots, $$
- 어떤 경우에, 이로부터 주기 수열을 얻을 수 있는지는 흥미로운 문제이다
불변량
- 점화식 \ref{lyn}에 의해 얻어진 수열 $\{x_n\}_{n\geq 0}$에 대하여, 다음은 $n\in \mathbb{Z}$에 의존하지 않는 불변량이다
\[C=(A+x_{n-1}+x_{n})\left(\frac{1}{x_{n-1}}+1\right) \left(\frac{1}{x_{n}}+1\right)\]
타원 곡선
- 점 $(x_0,y_0)$가 곡선 $F(x,y)=(x + 1) (y + 1) (x + y + A) - C x y=0$에 놓여 있는 경우, $(x_0',y_0')=(y,\frac{A+y}{x})$도 $F(x,y)=0$에 놓여 있다
- 타원곡선 $F(x,y)=(x + 1) (y + 1) (x + y + A) - C x y=0$을 통하여, 점화식 \ref{lyn}을 이해할 수도 있다
- 가령, 점화식 \ref{lyn}로부터 얻어지는 수열의 (최소)주기가 1,2,3,5,6,7,8,9,10,12가 되도록 하는 적당한 $x_0, x_1,A\in \mathbb{Q}$를 찾을 수 있으며, 다른 주기 (가령 4와 11)는 얻을 수 없다
특수한 경우
$A=1$
- 차분방정식의 해는 주기5인 주기수열이 되며, 5항 관계식 (5-term relation)에 등장함
$$ \alpha ,\beta ,\frac{1+\beta }{\alpha },\frac{1+\alpha +\beta }{\alpha \beta },\frac{1+\alpha }{\beta },\alpha ,\beta ,\cdots $$
$A=0$
- 다음과 같은 주기 6인 수열을 얻는다
$$ \alpha ,\beta ,\frac{\beta }{\alpha },\frac{1}{\alpha },\frac{1}{\beta },\frac{\alpha }{\beta },\alpha ,\beta ,\cdots $$
메모
- Pentagramma Mirificum
- http://www.jstor.org/stable/2324138
- We show that if $A \not= 1 $ then f is a twist map, with rotation numbers tending to 1/5 as the curves tend to infinity. Beukers and Cushman have shown that the rotation numbers are monotonic increasing if $A < 1,$ and decreasing if $A \gt 1.$ Using number theory we classify the periods of periodic orbits.
관련된 항목들
매스매티카 파일 및 계산 리소스
리뷰, 에세이, 강의노트
- Geometric Unfolding of a Difference Equation E. Christopher Zeeman, K.B., F.R.S. UT San Antonio, March 10, 1997 / Trinity University, March 17, 1997
관련논문
- Gasull, Armengol, Víctor Mañosa, and Xavier Xarles. 2012. “Rational Periodic Sequences for the Lyness Recurrence.” Discrete and Continuous Dynamical Systems. Series A 32 (2): 587–604. doi:10.3934/dcds.2012.32.587.
- Alperin, Roger C. 2011. “Integer Sequences Generated by $x_{n+1}=\frac {x^2_n+A}{x_{n-1}}$.” The Fibonacci Quarterly. The Official Journal of the Fibonacci Association 49 (4): 362–365. http://www.math.sjsu.edu/~alperin/IntegerA-Sequences.pdf
- Esch, J., and T. D. Rogers. 2001. “The Screensaver Map: Dynamics on Elliptic Curves Arising from Polygonal Folding.” Discrete & Computational Geometry. An International Journal of Mathematics and Computer Science 25 (3): 477–502. doi:10.1007/s004540010075.
- Bastien, G., and M. Rogalski. 2004. “Global Behavior of the Solutions of Lyness’ Difference Equation $u_{n+2}u_n=u_n+1+a$.” Journal of Difference Equations and Applications 10 (11): 977–1003. doi:10.1080/10236190410001728104.
- Beukers, F., and R. Cushman. 1998. “Zeeman’s Monotonicity Conjecture.” Journal of Differential Equations 143 (1): 191–200. doi:10.1006/jdeq.1997.3359.
- Lyness, R. C. 1961. “2952. Cycles.” The Mathematical Gazette 45 (353) (October 1): 207–209. doi:10.2307/3612778.
- Lyness, R. C. 1945. “1847. Cycles.” The Mathematical Gazette 29 (287) (December 1): 231–233. doi:10.2307/3609268.
- Lyness, R. C. 1942. “1581. Cycles.” The Mathematical Gazette 26 (268) (February 1): 62. doi:10.2307/3606036.