서로 접하는 네 원에 대한 데카르트의 정리와 아폴로니우스 개스킷

수학노트
둘러보기로 가기 검색하러 가기

데카르트의 정리

3214730-fourtangents.gif

  • 네 개의 원이 서로 접할때, 그 곡률(반지름의 역수) \(k_i\, (i=1,2,3,4)\) 이 만족시키는 관계\[\left( k_{1}+k_{2}+k_{3}+k_{s} \right)^{2} = 2\, \left( k_{1}^{2} + k_{2}^{2} + k_{3}^{2} + k_{s}^{2} \right)\]
  • 1643년 11월 데카르트의 편지


예 : 포드 원의 경우

포드 원 (Ford Circles)1.gif

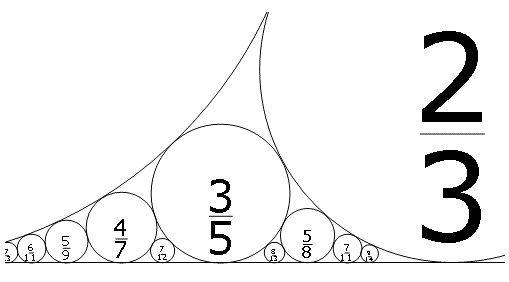
  • 서로 소인 두 자연수 p,q 에 대하여 C[p/q]를 중심이 \((\frac{p}{q},\frac{1}{2q^2})\) 이고, 반지름이 \(\frac{1}{2q^2}\)인 원이라 하자
  • C[3/5],C[5/8], C[2/3]와 x-축에 대하여 데카르트의 정리를 적용해 보자
  • 이 네 원은 서로서로 접하므로, 데카르트의 정리를 적용할 수 있다\[k_1=50,k_2=128,k_3=18, k_4=0\]\[50+128+18+0=196\], \(196^2=38416\)\[50^2+128^2+18^2+0^2=19208\], \(2\times 19208 = 38416\)
  • 포드 원에 대해서는 포드 원 (Ford Circles) 항목을 참조



소디의 시

  • 프레데릭 소디
    • 영국의 화학자, 1921년 노벨상 수상
  • 1936년 네이쳐에 'The Kiss Precise' 라는 시가 인쇄


The Kiss Precise by Frederick Soddy 

    For pairs of lips to kiss maybe 한쌍의 입술이 키스를 할땐     Involves no trigonometry. 삼각함수가 필요하지 않을꺼야.     'Tis not so when four circles kiss 하지만 네 원이 서로 키스를 할땐 그렇지 않지

   Each one the other three. 각각이 다른 셋과 함께.     To bring this off the four must be     As three in one or one in three.     If one in three, beyond a doubt     Each gets three kisses from without.     If three in one, then is that one     Thrice kissed internally.

    Four circles to the kissing come.     The smaller are the benter.     The bend is just the inverse of     The distance from the center.     Though their intrigue left Euclid dumb     There's now no need for rule of thumb.     Since zero bend's a dead straight line     And concave bends have minus sign,     The sum of the squares of all four bends     Is half the square of their sum.

    To spy out spherical affairs     An oscular surveyor     Might find the task laborious,     The sphere is much the gayer,     And now besides the pair of pairs     A fifth sphere in the kissing shares.     Yet, signs and zero as before,     For each to kiss the other four     The square of the sum of all five bends     Is thrice the sum of their squares.



아폴로니우스의 개스킷

3214730-600px-Apollonian gasket.svg.png

3214730-plan.gif



모듈라 군의 fundamental domain

3214730-modular.jpg



아폴로니우스 군(Appolonius group)

  • 데카르트의 공식을 2차 방정식으로 풀면 \(a_1=-a_1'+2a_2+2a_3+2a_4\)\[\mathbf{S_1} = \begin{pmatrix} -1 & 2 & 2 & 2 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\], \(\mathbf{S_2} = \begin{pmatrix} 0 & 1 & 0 & 0 \\ -1 & 2 & 2 & 2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)S_3,S_4
  • \(A=\langle S_1,S_2,S_3,S_4 \rangle\) 를 아폴로니우스 군이라 부름
  • \(Q(a_1,a_2,a_3,a_4)=2\sum a_i^2-(\sum a_i)^2\)는 signature (3,1) 인 이차형식
  • \(A=\langle S_1,S_2,S_3,S_4 \rangle\) 는 O_Q(\mathbb{Z}) 의 부분군 (orthogonal group)
  • A acts on H^3 (hyperbolic 3-space)
  • A is zariski dense in O_Q(\mathbb{C})


역사

  • BC200 아폴로니우스 - 서로 접하는 세 원이 있을때, 세 원이 접하는 두 개의 원이 있다
  • 1643 데카르트
  • 1937 소디 - 접하는 네 원의 곡률이 정수이면, 모든 원의 곡률은 정수이다


관련된 항목들


계산 리소스


사전형태의 자료

관련도서


관련논문



웹페이지와 관련링크


계산 리소스


블로그

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'descartes'}, {'LOWER': "'"}, {'LEMMA': 'theorem'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=서로_접하는_네_원에_대한_데카르트의_정리와_아폴로니우스_개스킷&oldid=52344"