수학과 지도학

지도와 수학

지도에는 한계가 있고, 용도에 따라서 저마다의 장단점이 있음.
- 지도제작의 한계에 대한 수학적 설명은 가우스의 놀라운 정리(Theorema Egregium) 항목을 참조.
메르카토르가 오래전에 항해용으로 만든 지도를, 열대지역의 국가의 면적이 작아졌다고 해서 서양중심주의라 비판하는 것은 착오.
수학공부를 통해, 지도 제작에 있는 그 한계를 이해하고, 세계의 모습에 대한 바른 생각을 갖는 것이 중요.

메르카토르 지도에 대한 간략한 소개

메르카토르 투영법으로 그려진 지도는, 면적을 희생하는 대신에 각도를 보존하는 성질을 갖는다
항정선(loxodrome 또는 Rhumb line) 이라 불리는 항해에 중요한 선을, 지도상에 직선으로 나타낼 수 있게 해주는, 항해용 지도로 16세기에 제작됨.
- 경선과의 각도가 일정한게 유지되는 곡선
극지방으로 갈수록, 그 위선들의 간격이 무한대에 가까워짐.
- 메르카토르 도법으로 만들어진 지도에서 그린랜드가 아프리카와 거의 같은 크기로 나타나는 이유(실제로는 훨씬 작다)
- 극지방을 지도에 표현하지 않음

경도와 위도

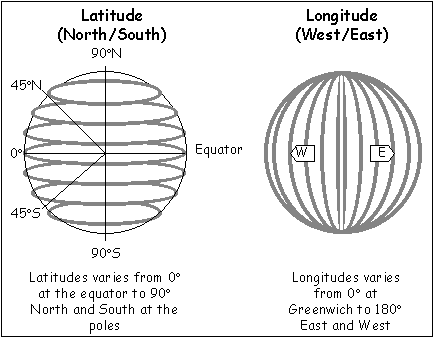
지도에서 중요한 정보가 위도와 경도라는 것이다.

위도는 위의 지도에서 왼쪽의 그림, 즉 적도에서부터 얼마나 북쪽 혹은 남쪽에 있는지를 재는 숫자이다. 영어로는 latitude라고 한다. 같은 위도상에 있는 지역들은 구면에서 원위에 놓이게 되는데, 이 원을 위선이라고 한다.
경도는 오른쪽 그림인데, 영국의 그리니치를 0으로 기준삼아, 얼마나 동쪽 혹은 서쪽에 있는지를 재는 숫자이다. 보다시피, 영어로는 longitude라고 한다. 같은 경도 상에 있는 지역들 은 북극과 남극을 지나는 대원에 의해 나타나게 되는데, 이 원을 경선이라고 부른다.

메르카토르 도법

메르카토르 지도는 위선과 경선을 서로 수직이 되는 직선들로 표현
경선을 그리는 방법
- 구면에서 일정한 간격으로 그려진 경선들을, 평면에 똑같이 일정한 간격으로 떨어져있는 y축과 평행한 직선들로 옮겨 그린다.
- 즉, 경선이 나타내는 경도가\(\phi\)라고 한다면, 평면지도에서는 \(x=\phi\) 인 직선으로 나타낸다는 것이다. 여기까지는 무척 쉽다.
위선을 그리는 방법

문제는 위도를 나타내는 위선들을 어떻게 지도에 그릴 것인가가 되겠다. 만약에 위도의 간격만큼 일정한 간격으로 지도에 위선들을 x축과 평행한 직선들로 나타내면, 문제가 발생한다.

이 그림에서 보다시피, 두 경선 사이의 간격은, 위도가 높아질수록 좁아져 극지방으로 가면 0에 가까워 진다. 그런데 이미 우리는 지도에 세로로 그어진 경선들을 그려놨다. 구면에서는 위도가 높아질수록 좁아지는 경선 사이의 간격을, 지도에서는 같게 보이도록 그려놓은 셈이다.

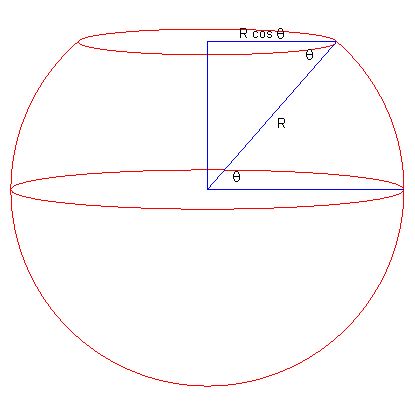
메르카토르 지도에서 원하는 것은 각도를 보존하는 것이다. 각도를 보존하는 것은 국소적인 작업인데, 이 각도를 보존하기 위해서는 국소적인 모양을 보존하도록 하면 된다. 위의 그림에서 나타나듯이, 위로 갈수록 좁은 경선 사이의 거리를 지도에서는 같게 보이도록 만들었다. 국소적인 모양을 보존하기 위해서는, 이렇게 가로의 좁은 거리를 더 길게 늘려준만큼, 세로의 길이도 늘려준 비율만큼 더 길게 해주어야 하는 것이다. 그러면 위도에 따라 이 비율이 어떻게 변하는가?

위의 그림이 말하는 바는, 구면에서 \(\theta+d\theta\)와 \(\theta\)를 나타내는 위선들의 간격이 \(\frac{1}{\cos\theta}d\theta=\sec\theta d\theta\) 만큼의 간격을 갖도록 해야 한다는 것이다. 즉 위도가 높아질수록, 위선들의 간격을 \(\sec\theta\) 배만큼 더 넓게 해준다는 것을 뜻한다.

이렇게 해주어야 국소적으로 지도의 모양이 보존되게 되고, 따라서 구면상의 각도가 지도에서도 보존되게 된다.

메르카토르 도법과 secant 함수의 적분

메르카토르는 지도를 만들때 어떻게 했는지 기록으로 남겨놓지 않았는데, 정밀한 미적분학의 툴이 없었으니, 아마도 실험적으로 간격을 어느 정도 넓힐 것인가를 수치적으로 계산해서 만들었다고 추측된다. 위의 그림과 식은, 1599년에 에드워드 라이트라는 사람이 메르카토르의 지도를 수학적으로 설명한 것이다.

그러나 에드워드 라이트의 때만해도 아직 미적분학이 없어서 적분을 몰랐으니, 에드워드 라이트는 위선들의 지도에서의 y축 좌표를, 말하자면 이런 식으로 표현했다. 만약에 위선들을 1도 간격으로 그리고, 구면에서 1도만큼의 거리를 \(\Delta\)라고 한다면,

위도	메르카토르 지도에서의 y좌표
0도	0
1도	(sec 1도) x \(\Delta\)
2도	(sec 1도+sec 2도) x \(\Delta\)
3도	(sec 1도+sec 2도+sec 3도) x \(\Delta\)
4도	(sec 1도+sec 2도+sec 3도+sec 4도) x \(\Delta\)

이렇게 한다는 것이다. 그때만 해도 적분이 없었기 때문에! 그는 그렇게 이러한 계산이 담긴 표를 출판한 것이다.

이 표는 메르카토르 도법이 구분구적법에 의한 정적분문제와 같아. 즉 위의 표는 본질적으로 다음과 같은 표이다.

위도	지도에서 y좌표
\(\theta\)	\(\int_{0}^{\theta} {\sec x} dx\)

1614년 네이피어가 로그를 발견하고, 로그표를 출판한다. 로그표가 있으면, 곱하기를 더하기로 대신할 수 있고, 나누기를 빼기로 대신할 수 있다. 이 생각은 처음에는 매우 바보같아 보이지만, 컴퓨터가 없던 당시, 천문학의 혁명기에, 큰 숫자를 쉽게 다룰 수 있게 해준 위대한 발명이었던 것이다. 큰 수의 제곱근, 세제곱근도 쉽게 구할 수 있고, 제곱, 세제곱도 쉽게 구 할 수 있게 된다.

1620년에는 에드문트 군터라는 자가 삼각함수의 로그가 담긴 표를 출판한다.

1640년대, 헨리 본드라는 사람이 라이트의 위도 테이블이 \( \ln \tan (\frac{\theta}{2}+\frac{\pi}{4})\) 의 값과 일치한다는 사실을 발견한다. 도대체 이 두 값이 왜 일치하는 것일까? 이 문제가 위에서 언급했던 당대의 중요 미해결문제가 된 것이다. 당시는 미적분학의 언어가 한참 개발되던 시기였다. 이제 지금까지 한 것을, 미적분학의 언어로 표현하자면,

\(\int_{0}^{\theta} {\sec x} dx= \ln (\sec \theta+ \tan \theta) = \ln \tan (\frac{\theta}{2}+\frac{\pi}{4})\)

지도에서 발생한 문제가 시컨트 함수의 적분 문제를 먼저 추측한 것이니, 참 재밌는 일이 아닌가? 그리하여 이 적분문제가 위의 의미로 증명되고 출판된 것이 1660~70년대였으니, 정확히 메르카토르 지도로부터 백년이 걸린 것이다.

재미있는 사실

2001년에 방송됐던, 웨스트윙 시즌 2의 16화 “Somebody’s Going to Emergency, Somebody’s Going to Jail” 에서는 메르카토르 도법으로 만들어진 지도와 피터스 도법으로 만들어진 지도가 비교되는 장면이 나온다.
http://sci.tech-archive.net/Archive/sci.math/2009-02/msg03894.html

메모

Cartographical Map Projections

매스매티카 코드

사전형태의 자료

블로그

완벽한 세계지도? 박부성, 네이버 오늘의 과학, 2009-4-28
피타고라스의 창,
- 지도의 기하학
- 메르카토르 지도에 얽힌 수학의 역사

수학과 지도학

목차

지도와 수학

메르카토르 지도에 대한 간략한 소개

경도와 위도

메르카토르 도법

메르카토르 도법과 secant 함수의 적분

재미있는 사실

메모

관련된 항목들

매스매티카 코드

사전형태의 자료

관련도서

관련논문

관련기사

블로그

메타데이터

위키데이터

Spacy 패턴 목록

둘러보기 메뉴

검색