나비정리
둘러보기로 가기
검색하러 가기
개요
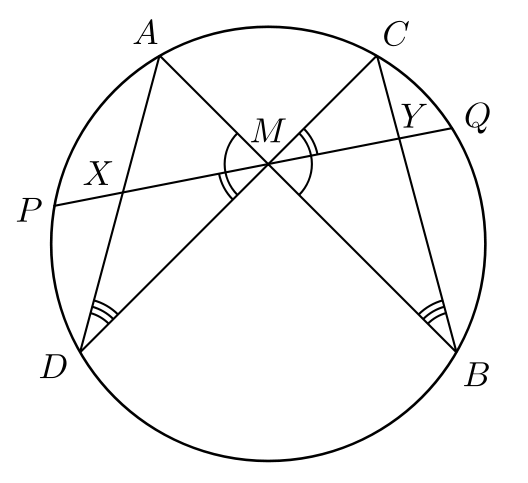
- 현PQ의 중점 M을 잡는다.
- 원주위의 두 점, A, C 에서 각각 M을 지나는 선을 그어 원과 만나는 점을 B,D라 한다.
- 그 다음 AD와 PQ가 만나는 점을 X, CB와 PQ가 만나는 점을 Y라 하면, M은 XY의 중점이다.
증명
나비 정리의 증명은 여러가지가 있으나 그 중 가장 대표적인 증명을 소개하도록 하겠다.
선분 PQ 의 수직 이등분선에 대한 점 B 의 선대칭점 B' 을 생각하면 그 점은 원주 위에 놓이게 된다. 따라서, 선대칭 성질에 의해 삼각형 MBB' 은 이등변 삼각형이 되므로 MB' = MB 가 된다. 또한, BB' 과 PQ 가 평행하므로 ∠ XMB' = ∠ MB'B = ∠ MBB' = ∠ BMY 가 되므로 ∠ XMB' = ∠ BMY 이다.
또한, 사각형 ADB'B 는 한 원위에 네 점이므로 ∠ ADB' + ∠ABB' = 180 인데, ∠ ABB' = ∠ XMB' 이므로 ∠ ADB' + ∠ XMB' = 180. 따라서, X, D, B', M 도 한 원위에 네 점이 된다. 그러므로 ∠ MBY = ∠ XDM = ∠ XB'M (원주각)
결과적으로, 삼각형 XB'M 과 삼각형 YBM 은 ASA 합동. 따라서, XM = YM.
관련된 단원
관련된 다른 주제들
관련도서
관련된 고교수학 또는 대학수학
참고할만한 자료
- 나비 정리
- 고봉균
- 매쓰레터 172호
- 평면 기하의 아이디어
- 위키피디아
동영상 강좌
- Butterfly theorem, animated proof
- Antonio Gutierrez
- Geometry Step by Step from the Land of the Incas
- proof_of_the_Butterfly_theorem_using_cross_ration.pdf
메타데이터
위키데이터
- ID : Q377047
Spacy 패턴 목록
- [{'LOWER': 'butterfly'}, {'LEMMA': 'theorem'}]