미적분학 입문

삼각형의 넓이 공식

<math>S=\frac{1}{2}bh</math>

<math>1+2+\cdots+n = \frac{n(n+1)}{2}=\frac{1}{2}n^2+\cdots</math>

적분

<math>\int x\,dx = \frac{1}{2}x^2+C</math>

---

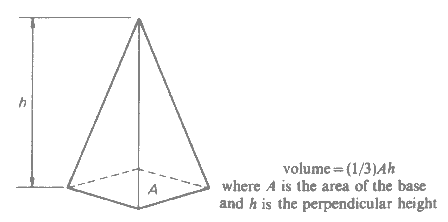
부피공식

<math>V=\frac{1}{3}Ah</math>

<math>1^2 + 2^2 + 3^2 + \cdots + n^2 = {n(n+1)(2n+1) \over 6} = {2n^3 + 3n^2 + n \over 6}=\frac{1}{3}n^3+\cdots</math>

적분

<math>\int x^2\,dx = \frac{1}{3}x^3+C</math>

---

이 다음에 와야 할 것들은???

더 읽어볼 것들

• 거듭제곱의 합을 구하는 공식
• 각뿔의 부피는?
  • 박부성, 네이버캐스트, 2009-3-31