이진법
둘러보기로 가기
검색하러 가기
예
- 아래는 1부터 16까지의 자연수를 2진법으로 표현한 것이다
\[ \begin{array}{c|c|c} n & & \\ \hline 1 & 1 & 1_2 \\ 2 & 2 & 10_2 \\ 3 & 1+2 & 11_2 \\ 4 & 2^2 & 100_2 \\ 5 & 1+2^2 & 101_2 \\ 6 & 2+2^2 & 110_2 \\ 7 & 1+2+2^2 & 111_2 \\ 8 & 2^3 & 1000_2 \\ 9 & 1+2^3 & 1001_2 \\ 10 & 2+2^3 & 1010_2 \\ 11 & 1+2+2^3 & 1011_2 \\ 12 & 2^2+2^3 & 1100_2 \\ 13 & 1+2^2+2^3 & 1101_2 \\ 14 & 2+2^2+2^3 & 1110_2 \\ 15 & 1+2+2^2+2^3 & 1111_2 \\ 16 & 2^4 & 10000_2 \end{array} \]
마법의 카드
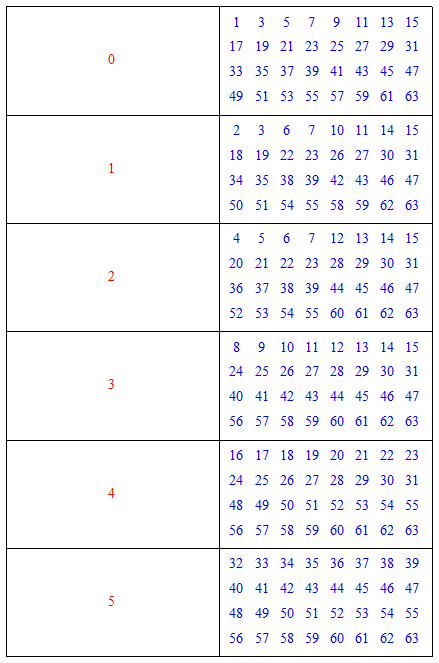
- 마법의 카드 (이진법의 원리를 이용한 놀이 학습)
- 상대에게 1에서 63까지의 수 중에서 하나를 선택한 후, 그 수가 들어있는 카드를 전부 알려달라고 한다
- 선택한 수는 카드에서 가장 작은 수들을 더하여 얻어낼 수 있다
- 가령 숫자 38은 카드 1,2,5에 들어 있다.
- 카드 1,2,5에서 가장 작은 수는 각각 2,4,32이고, 2+4+32=38이 성립한다
- 이는 8-90년대에 초등학생을 위한 방학용 학습 교재인 탐구생활에도 소개된 바 있다