"히포크라테스의 초승달"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| (같은 사용자의 중간 판 3개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | == | + | ==작도와 구적가능성== |
* 구적이란 주어진 도형의 면적을 구하는 대신, 같은 면적을 갖는 정사각형을 작도하는 것. | * 구적이란 주어진 도형의 면적을 구하는 대신, 같은 면적을 갖는 정사각형을 작도하는 것. | ||
* 평면도형이 구적가능하다는 것은 자와 컴파스로 같은 면적을 갖는 정사각형을 작도할 수 있다는 말. | * 평면도형이 구적가능하다는 것은 자와 컴파스로 같은 면적을 갖는 정사각형을 작도할 수 있다는 말. | ||
| − | * [[작도문제와 구적가능성]] | + | * [[작도문제와 구적가능성]] 에서 간략하게 소개되어 있음 |
| − | + | ||
| − | + | ||
==히포크라테스의 초승달== | ==히포크라테스의 초승달== | ||
| 18번째 줄: | 18번째 줄: | ||
어두운 초승달 영역의 넓이와, 삼각형 OAB의 넓이가 같다 | 어두운 초승달 영역의 넓이와, 삼각형 OAB의 넓이가 같다 | ||
| − | * 이 | + | * 이 사실의 증명은 피타고라스의 정리를 사용 |
| − | + | ||
| − | + | ||
==구적가능한 초승달== | ==구적가능한 초승달== | ||
* 초승달이란 두 원의 호 (arc)로 둘러싸인 영역을 의미 | * 초승달이란 두 원의 호 (arc)로 둘러싸인 영역을 의미 | ||
* 두 부채꼴의 중심각의 비율을 u라 두면, 초승달은 다음의 다섯 가지 경우에만 구적가능 | * 두 부채꼴의 중심각의 비율을 u라 두면, 초승달은 다음의 다섯 가지 경우에만 구적가능 | ||
| − | + | :<math> | |
u=3/2,5/3,2,3,5 | u=3/2,5/3,2,3,5 | ||
| − | + | </math> | |
| − | * 이는 다음의 방정식을 풀어 얻어지는 | + | * 이는 다음의 방정식을 풀어 얻어지는 <math>\sin \theta</math>가 작도가능하다는 조건으로부터 얻어진다 |
| − | + | :<math> | |
\left(\frac{\sin u\theta}{\sin \theta}\right)^2=u | \left(\frac{\sin u\theta}{\sin \theta}\right)^2=u | ||
| − | + | </math> | |
* 아래의 그림에서 작은 원의 반지름은 1로 고정함 | * 아래의 그림에서 작은 원의 반지름은 1로 고정함 | ||
| − | === | + | ===<math>u=3/2</math>=== |
| − | * 초승달의 넓이: | + | * 초승달의 넓이: <math>\frac{1}{4} \sqrt{\frac{3}{2} \left(9-\sqrt{33}\right)} = 0.552447\cdots</math> |
| − | * 두 부채꼴의 각도 : | + | * 두 부채꼴의 각도 : <math>160.874^{\circ}, 107.25^{\circ}</math> |
[[파일:히포크라테스의 초승달1.png]] | [[파일:히포크라테스의 초승달1.png]] | ||
| − | === | + | ===<math>u=5/3</math>=== |
| − | * 초승달의 넓이: | + | * 초승달의 넓이: <math>\frac{1}{6} \sqrt{25-5 \sqrt{25-6 \sqrt{15}}} = 0.714197\cdots</math> |
| − | * 두 부채꼴의 각도 : | + | * 두 부채꼴의 각도 : <math>167.939^{\circ}, 100.764^{\circ}</math> |
[[파일:히포크라테스의 초승달2.png]] | [[파일:히포크라테스의 초승달2.png]] | ||
| − | === | + | ===<math>u=2</math>=== |
| − | * 초승달의 넓이: | + | * 초승달의 넓이: <math>1</math> |
| − | * 두 부채꼴의 각도 : | + | * 두 부채꼴의 각도 : <math>180^{\circ}, 90^{\circ}</math> |
[[파일:히포크라테스의 초승달3.png]] | [[파일:히포크라테스의 초승달3.png]] | ||
| − | === | + | ===<math>u=3</math>=== |
| − | * 초승달의 넓이: | + | * 초승달의 넓이: <math>\frac{3^{3/4}}{\sqrt{2}} = 1.61185\cdots</math> |
| − | * 두 부채꼴의 각도 : | + | * 두 부채꼴의 각도 : <math>205.588^{\circ}, 68.5293^{\circ}</math> |
[[파일:히포크라테스의 초승달4.png]] | [[파일:히포크라테스의 초승달4.png]] | ||
| − | === | + | ===<math>u=5</math>=== |
| − | * 초승달의 넓이: | + | * 초승달의 넓이: <math>\frac{1}{2} \sqrt{\frac{5}{2} \left(-5+\sqrt{25+64 \sqrt{5}}\right)} = 2.23126\cdots</math> |
| − | * 두 부채꼴의 각도 : | + | * 두 부채꼴의 각도 : <math>234.391^{\circ}, 46.8783^{\circ}</math> |
[[파일:히포크라테스의 초승달5.png]] | [[파일:히포크라테스의 초승달5.png]] | ||
| − | + | ||
==관련된 항목들== | ==관련된 항목들== | ||
| 82번째 줄: | 82번째 줄: | ||
==매스매티카 파일 및 계산 리소스== | ==매스매티카 파일 및 계산 리소스== | ||
* https://docs.google.com/file/d/0B8XXo8Tve1cxZktyNmVoQkJTNzg/edit | * https://docs.google.com/file/d/0B8XXo8Tve1cxZktyNmVoQkJTNzg/edit | ||
| − | + | ||
==사전형태의 자료== | ==사전형태의 자료== | ||
| 89번째 줄: | 89번째 줄: | ||
* http://en.wikipedia.org/wiki/Lune_of_Hippocrates | * http://en.wikipedia.org/wiki/Lune_of_Hippocrates | ||
| − | + | ||
==관련도서== | ==관련도서== | ||
| 97번째 줄: | 97번째 줄: | ||
** William Dunham | ** William Dunham | ||
| − | + | ||
==리뷰논문, 에세이, 강의노트== | ==리뷰논문, 에세이, 강의노트== | ||
| 109번째 줄: | 109번째 줄: | ||
[[분류:원주율]] | [[분류:원주율]] | ||
[[분류:추상대수학]] | [[분류:추상대수학]] | ||
| + | |||
| + | ==메타데이터== | ||
| + | ===위키데이터=== | ||
| + | * ID : [https://www.wikidata.org/wiki/Q312629 Q312629] | ||
| + | ===Spacy 패턴 목록=== | ||
| + | * [{'LOWER': 'hippocrates'}, {'LOWER': 'of'}, {'LEMMA': 'chio'}] | ||
2021년 2월 17일 (수) 02:30 기준 최신판
작도와 구적가능성
- 구적이란 주어진 도형의 면적을 구하는 대신, 같은 면적을 갖는 정사각형을 작도하는 것.
- 평면도형이 구적가능하다는 것은 자와 컴파스로 같은 면적을 갖는 정사각형을 작도할 수 있다는 말.
- 작도문제와 구적가능성 에서 간략하게 소개되어 있음
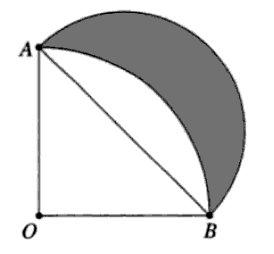
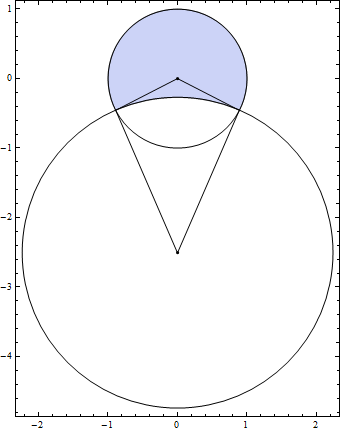
히포크라테스의 초승달
- 히포크라테스는 BC440년경, 다음과 같은 발견으로 원의 구적문제가 해결 가능할지도 모른다는 희망을 남김.
- 정리
어두운 초승달 영역의 넓이와, 삼각형 OAB의 넓이가 같다
- 이 사실의 증명은 피타고라스의 정리를 사용
구적가능한 초승달
- 초승달이란 두 원의 호 (arc)로 둘러싸인 영역을 의미
- 두 부채꼴의 중심각의 비율을 u라 두면, 초승달은 다음의 다섯 가지 경우에만 구적가능
\[ u=3/2,5/3,2,3,5 \]
- 이는 다음의 방정식을 풀어 얻어지는 \(\sin \theta\)가 작도가능하다는 조건으로부터 얻어진다
\[ \left(\frac{\sin u\theta}{\sin \theta}\right)^2=u \]
- 아래의 그림에서 작은 원의 반지름은 1로 고정함
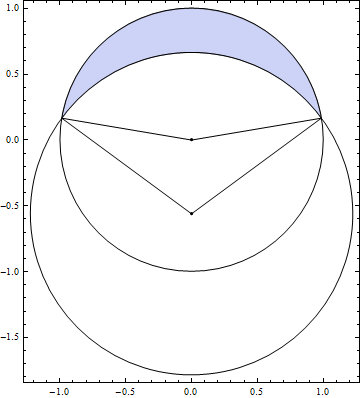
\(u=3/2\)
- 초승달의 넓이\[\frac{1}{4} \sqrt{\frac{3}{2} \left(9-\sqrt{33}\right)} = 0.552447\cdots\]
- 두 부채꼴의 각도 \[160.874^{\circ}, 107.25^{\circ}\]
\(u=5/3\)
- 초승달의 넓이\[\frac{1}{6} \sqrt{25-5 \sqrt{25-6 \sqrt{15}}} = 0.714197\cdots\]
- 두 부채꼴의 각도 \[167.939^{\circ}, 100.764^{\circ}\]
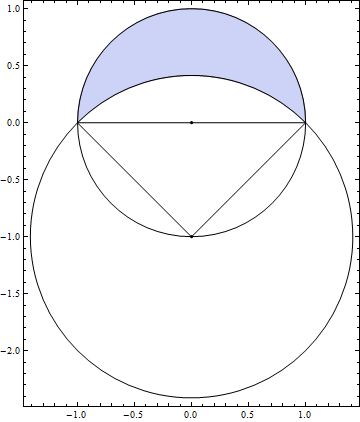
\(u=2\)
- 초승달의 넓이\[1\]
- 두 부채꼴의 각도 \[180^{\circ}, 90^{\circ}\]
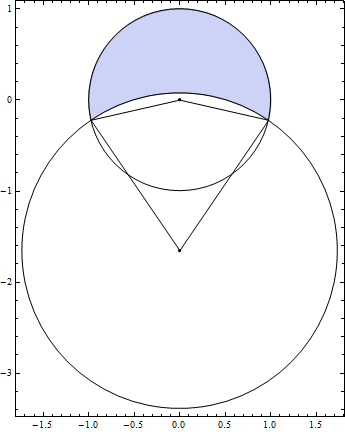
\(u=3\)
- 초승달의 넓이\[\frac{3^{3/4}}{\sqrt{2}} = 1.61185\cdots\]
- 두 부채꼴의 각도 \[205.588^{\circ}, 68.5293^{\circ}\]
\(u=5\)
- 초승달의 넓이\[\frac{1}{2} \sqrt{\frac{5}{2} \left(-5+\sqrt{25+64 \sqrt{5}}\right)} = 2.23126\cdots\]
- 두 부채꼴의 각도 \[234.391^{\circ}, 46.8783^{\circ}\]
관련된 항목들
관련된 고교수학 또는 대학수학
매스매티카 파일 및 계산 리소스
사전형태의 자료
관련도서
- Journey through Genius: The Great Theorems of Mathematics
- Chapter 1. Hippocrates' Quadrature of the Lune
- William Dunham
리뷰논문, 에세이, 강의노트
- The Five Squarable Lunes
- Postnikov, M. M., and Abe Shenitzer. 2000. “The Problem of Squarable Lunes.” The American Mathematical Monthly 107 (7) (August 1): 645–651. http://dx.doi.org/10.2307/2589121
- Girstmair, Kurt. 2003. “Hippocrates’ Lunes and Transcendence.” Expositiones Mathematicae 21 (2): 179–183. http://dx.doi.org/10.1016/S0723-0869(03)80018-X
- Chebotarev and his density theorem P. Stevenhagen and H. W. Lenstra, Jr
메타데이터
위키데이터
- ID : Q312629
Spacy 패턴 목록
- [{'LOWER': 'hippocrates'}, {'LOWER': 'of'}, {'LEMMA': 'chio'}]