"포드 원 (Ford Circles)"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
|||
| (사용자 2명의 중간 판 20개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | < | + | ==개요== |
| + | * <math>p,q</math>가 서로 소인 자연수일 때, 중심이 <math>(\frac{p}{q},\frac{1}{2q^2})</math> 이고, 반지름이 <math>\frac{1}{2q^2}</math>인 원을 포드 원이라 함 | ||
| + | * <math>x</math>-축에 접한다 | ||
| − | + | [[파일:포드 원 (Ford Circles)1.gif]] | |
| − | |||
| − | + | ==관찰== | |
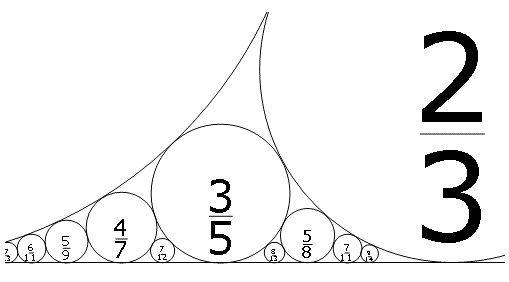
| + | * 위 그림을 잘 보면서 관찰해 보자. (원 안에 적혀 있는 숫자는, 원 중심의 <math>x</math> 좌표이다.) | ||
| + | * <math>p,q</math>가 서로소인 자연수이므로, 원 중심의 <math>x</math> 좌표들은 기약분수이다. | ||
| + | * 서로 다른 두 포드 원은 만나지 않거나, 접한다. | ||
| + | * 접하는 두 포드 원 사이에는 어떤 관계가 있을까? | ||
| + | ** <math>\frac35 , \frac23</math> | ||
| + | ** <math>\frac35 , \frac58</math> | ||
| + | ** <math>\frac58, \frac23</math> | ||
| + | ** <math>\frac58, \frac{7}{11}</math> | ||
| + | * 서로 접하는 세 포드 원 사이에는 어떤 관계가 있을까 | ||
| + | ** <math>\frac35, \frac58 , \frac23</math> | ||
| + | ** <math>\frac35, \frac{8}{13} , \frac58</math> | ||
| + | ** <math>\frac58, \frac{7}{11} , \frac23</math> | ||
| + | ** <math>\frac47, \frac{7}{12} , \frac35</math> | ||
| + | * [[패리 수열(Farey series)]] | ||
| − | + | ==관찰의 증명== | |
| − | + | ;정리 | |
| + | 두 포드 원은 만나지 않거나, 접한다. | ||
| − | + | ;증명 | |
| − | |||
| − | + | 아래에 서로 다른 두 개의 포드 원을 그렸다. 원 A 는 중심의 <math>x</math> 좌표가 <math>p/q</math> 인 원이고, 원 B 는 중심의 <math>x</math> 좌표가 <math>P/Q</math> 인 원이다. (<math>p,q, P, Q</math> 는 자연수, <math>gcd(p,q) = gcd(P, Q) = 1</math>) | |
| − | + | [[파일:포드 원 (Ford Circles)3.gif]] | |
| − | < | + | |
| − | + | 위 그림에서, 점 <math>A</math> 에서 선분 <math>\overline{BG}</math> 위에 내린 발을 <math>C</math> 라 하자. 그러면 삼각형 <math>\triangle ACB</math> 는 직각삼각형이 된다. 피타고라스의 정리를 적용하면, | |
| − | |||
| − | |||
| − | |||
| − | + | <math>\overline{AB}^2 = \overline{BC}^2 + \overline{CA}^2</math> 이다. 포드 원의 정의에서 <math>A(\frac{p}{q}, \frac{1}{2q^2}), B(\frac{P}{Q}, \frac{1}{2Q^2}), C(\frac{P}{Q},\frac{1}{2q^2} )</math> 이므로, 다음이 성립한다 | |
| − | + | :<math> | |
| − | + | \overline{AB}^2 = (\overline{AD} + \overline{EB})^2 + \frac{(Pq - pQ)^2 - 1}{Q^2 q^2} | |
| − | + | </math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 여기서, | |
| − | + | i. <math>|Pq -pQ|> 1</math> 이면, <math>\overline{AB} > \overline{AD} + \overline{EB}</math> 이므로, 두 원은 서로 떨어져 있다. | |
| − | + | ii. <math>|Pq -pQ|= 1</math> 이면, <math>\overline{AB} = \overline{AD} + \overline{EB}</math> 이므로, 두 원은 접한다. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ii. | ||
iii. <math>|Pq -pQ| <1</math> 일 수는 없다. | iii. <math>|Pq -pQ| <1</math> 일 수는 없다. | ||
| − | + | 왜냐하면, <math>p,q, P, Q</math> 는 자연수이므로 <math>Pq -pQ = 0</math> 이면, <math>p/q \ne P/Q</math> 에 모순이기 때문이다. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 위 세 가지 경우에서, 서로 겹쳐 있는 두 포드 원은 없음을 알 수 있다. ■ | |
| − | |||
| − | + | ;정리 | |
| + | <math>x</math> 좌표가 <math>p/q</math> 인 포드 원을 <math>C[p/q]</math> 라고 쓰자. 두 포드 원 <math>C[b/a]</math> 과 <math>C[d/c]</math>이 접하면, <math>|ad - bc| = 1</math> 이 성립한다. | ||
| − | + | ;증명 | |
| − | + | 관찰 1 의 증명 중 ii) 로부터 알 수 있다. ■ | |
3. Farey Series 와의 관계 | 3. Farey Series 와의 관계 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==메모== | |
| + | [[파일:포드 원 (Ford Circles)2.gif]] | ||
| − | |||
| − | |||
| − | + | ==관련된 항목들== | |
| − | * [[패리 수열(Farey series) | + | * [[패리 수열(Farey series)]] |
| − | * [[모듈라 군 | + | * [[모듈라 군, j-invariant and the singular moduli]] |
| − | + | * [[모듈라 군(modular group)]] | |
| + | * [[연분수와 유리수 근사]] | ||
| − | + | ||
| − | + | ==매스매티카 파일 및 계산 리소스== | |
| − | * | + | * https://drive.google.com/file/d/0B8XXo8Tve1cxNmU5NDhlZGMtYWU5MS00YThiLWFiZjEtNjk4N2FmZWI5ZmQy/view |
| − | + | * http://mathematica.stackexchange.com/questions/100628/wiggly-and-imprecise-animated-gif-output | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==사전형태의 자료== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* http://en.wikipedia.org/wiki/Ford_circles | * http://en.wikipedia.org/wiki/Ford_circles | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | ==리뷰, 에세이, 강의노트== | ||
| − | * | + | * 애기똥풀, [[파일:3210238-Ford Circle.pdf]] |
| − | + | * 이광연, [http://navercast.naver.com/science/math/1049 바보셈에서 페리수열], 네이버 오늘의 과학, 2009년 9월 8일 | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | < | + | ==관련논문== |
| + | * Athreya, Jayadev, Sneha Chaubey, Amita Malik, and Alexandru Zaharescu. “Geometry of Farey-Ford Polygons.” arXiv:1410.4908 [math], October 18, 2014. http://arxiv.org/abs/1410.4908. | ||
| + | * [http://www.jstor.org/stable/2302799 Fractions] L. R. Ford, <cite>The American Mathematical Monthly</cite>, Vol. 45, No. 9 (Nov., 1938), pp. 586-601 | ||
| − | * | + | ==메타데이터== |
| − | * | + | ===위키데이터=== |
| + | * ID : [https://www.wikidata.org/wiki/Q1436714 Q1436714] | ||
| + | ===Spacy 패턴 목록=== | ||
| + | * [{'LOWER': 'ford'}, {'LEMMA': 'circle'}] | ||
2021년 2월 17일 (수) 05:06 기준 최신판
개요
- \(p,q\)가 서로 소인 자연수일 때, 중심이 \((\frac{p}{q},\frac{1}{2q^2})\) 이고, 반지름이 \(\frac{1}{2q^2}\)인 원을 포드 원이라 함
- \(x\)-축에 접한다
관찰
- 위 그림을 잘 보면서 관찰해 보자. (원 안에 적혀 있는 숫자는, 원 중심의 \(x\) 좌표이다.)
- \(p,q\)가 서로소인 자연수이므로, 원 중심의 \(x\) 좌표들은 기약분수이다.
- 서로 다른 두 포드 원은 만나지 않거나, 접한다.
- 접하는 두 포드 원 사이에는 어떤 관계가 있을까?
- \(\frac35 , \frac23\)
- \(\frac35 , \frac58\)
- \(\frac58, \frac23\)
- \(\frac58, \frac{7}{11}\)
- 서로 접하는 세 포드 원 사이에는 어떤 관계가 있을까
- \(\frac35, \frac58 , \frac23\)
- \(\frac35, \frac{8}{13} , \frac58\)
- \(\frac58, \frac{7}{11} , \frac23\)
- \(\frac47, \frac{7}{12} , \frac35\)
- 패리 수열(Farey series)
관찰의 증명
- 정리
두 포드 원은 만나지 않거나, 접한다.
- 증명
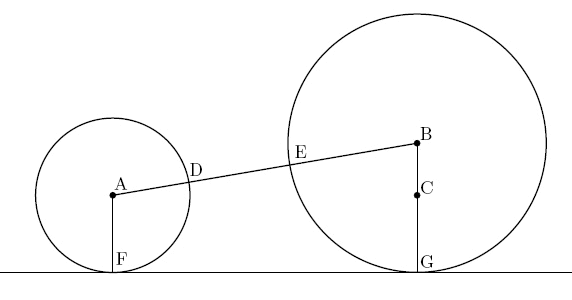
아래에 서로 다른 두 개의 포드 원을 그렸다. 원 A 는 중심의 \(x\) 좌표가 \(p/q\) 인 원이고, 원 B 는 중심의 \(x\) 좌표가 \(P/Q\) 인 원이다. (\(p,q, P, Q\) 는 자연수, \(gcd(p,q) = gcd(P, Q) = 1\))
위 그림에서, 점 \(A\) 에서 선분 \(\overline{BG}\) 위에 내린 발을 \(C\) 라 하자. 그러면 삼각형 \(\triangle ACB\) 는 직각삼각형이 된다. 피타고라스의 정리를 적용하면,
\(\overline{AB}^2 = \overline{BC}^2 + \overline{CA}^2\) 이다. 포드 원의 정의에서 \(A(\frac{p}{q}, \frac{1}{2q^2}), B(\frac{P}{Q}, \frac{1}{2Q^2}), C(\frac{P}{Q},\frac{1}{2q^2} )\) 이므로, 다음이 성립한다 \[ \overline{AB}^2 = (\overline{AD} + \overline{EB})^2 + \frac{(Pq - pQ)^2 - 1}{Q^2 q^2} \]
여기서,
i. \(|Pq -pQ|> 1\) 이면, \(\overline{AB} > \overline{AD} + \overline{EB}\) 이므로, 두 원은 서로 떨어져 있다.
ii. \(|Pq -pQ|= 1\) 이면, \(\overline{AB} = \overline{AD} + \overline{EB}\) 이므로, 두 원은 접한다.
iii. \(|Pq -pQ| <1\) 일 수는 없다.
왜냐하면, \(p,q, P, Q\) 는 자연수이므로 \(Pq -pQ = 0\) 이면, \(p/q \ne P/Q\) 에 모순이기 때문이다.
위 세 가지 경우에서, 서로 겹쳐 있는 두 포드 원은 없음을 알 수 있다. ■
- 정리
\(x\) 좌표가 \(p/q\) 인 포드 원을 \(C[p/q]\) 라고 쓰자. 두 포드 원 \(C[b/a]\) 과 \(C[d/c]\)이 접하면, \(|ad - bc| = 1\) 이 성립한다.
- 증명
관찰 1 의 증명 중 ii) 로부터 알 수 있다. ■
3. Farey Series 와의 관계
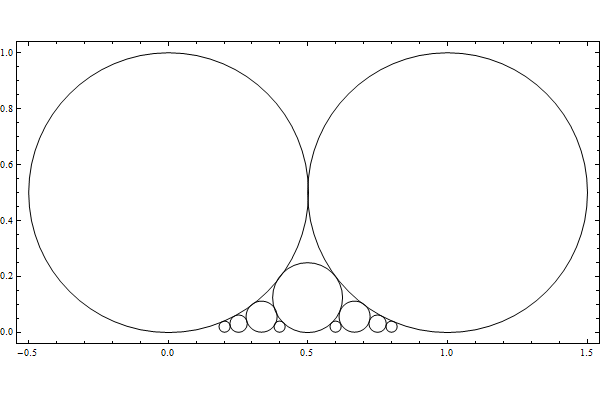
메모
관련된 항목들
매스매티카 파일 및 계산 리소스
- https://drive.google.com/file/d/0B8XXo8Tve1cxNmU5NDhlZGMtYWU5MS00YThiLWFiZjEtNjk4N2FmZWI5ZmQy/view
- http://mathematica.stackexchange.com/questions/100628/wiggly-and-imprecise-animated-gif-output
사전형태의 자료
리뷰, 에세이, 강의노트
- 애기똥풀, 파일:3210238-Ford Circle.pdf
- 이광연, 바보셈에서 페리수열, 네이버 오늘의 과학, 2009년 9월 8일
관련논문
- Athreya, Jayadev, Sneha Chaubey, Amita Malik, and Alexandru Zaharescu. “Geometry of Farey-Ford Polygons.” arXiv:1410.4908 [math], October 18, 2014. http://arxiv.org/abs/1410.4908.
- Fractions L. R. Ford, The American Mathematical Monthly, Vol. 45, No. 9 (Nov., 1938), pp. 586-601
메타데이터
위키데이터
- ID : Q1436714
Spacy 패턴 목록
- [{'LOWER': 'ford'}, {'LEMMA': 'circle'}]