"가우스의 렘니스케이트 상수"의 두 판 사이의 차이

수학노트
둘러보기로 가기 검색하러 가기
 
(같은 사용자의 중간 판 5개는 보이지 않습니다)
1번째 줄: 1번째 줄:
 
==개요==
 
==개요==
−
* 렘니스케이트 상수 $\omega$를 다음과 같이 정의
+
* 렘니스케이트 상수 <math>\omega</math>를 다음과 같이 정의
 
:<math>\omega:=2\int_0^1\frac{dx}{\sqrt{1-x^4}}=2.622057554292\cdots</math>
 
:<math>\omega:=2\int_0^1\frac{dx}{\sqrt{1-x^4}}=2.622057554292\cdots</math>
 
* 다음과 같이 쓸 수 있다
 
* 다음과 같이 쓸 수 있다
−
$$
+
:<math>
 
2\omega=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}}
 
2\omega=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}}
−
$$
+
</math>
−
여기서 $B$는 [[오일러 베타적분(베타함수)]]이고, $\Gamma$는 [[감마함수]]
+
여기서 <math>B</math>는 [[오일러 베타적분(베타함수)]]이고, <math>\Gamma</math>는 [[감마함수]]
 
* [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분|렘니스케이트 곡선의 둘레의 길이]]의 절반에 해당
 
* [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분|렘니스케이트 곡선의 둘레의 길이]]의 절반에 해당
 
* [[타원곡선 y²=x³-x]]의 주기([[periods]])이며 [[무리수와 초월수|초월수]]임
 
* [[타원곡선 y²=x³-x]]의 주기([[periods]])이며 [[무리수와 초월수|초월수]]임
12번째 줄: 12번째 줄:
  
 
==데데킨트 제타함수의 미분==
 
==데데킨트 제타함수의 미분==
−
* 수체 $K=\mathbb{Q}(\sqrt{-1})$의 [[데데킨트 제타함수]]
+
* 수체 <math>K=\mathbb{Q}(\sqrt{-1})</math>의 [[데데킨트 제타함수]]
 
;정리
 
;정리
−
$$
+
:<math>
 
\zeta_K'(0)=-\frac{1}{4}\log\left(\frac{\Gamma(\frac{1}{4})^4}{4\pi}\right)=-\frac{1}{4}\log 2\omega^2
 
\zeta_K'(0)=-\frac{1}{4}\log\left(\frac{\Gamma(\frac{1}{4})^4}{4\pi}\right)=-\frac{1}{4}\log 2\omega^2
−
$$
+
</math>
 
;증명
 
;증명
−
[[이차 수체의 데데킨트 제타함수]]에서 $\zeta_K(s)$는 다음과 같이 분해됨을 보였다
+
[[이차 수체의 데데킨트 제타함수]]에서 <math>\zeta_K(s)</math>는 다음과 같이 분해됨을 보였다
−
$$
+
:<math>
 
\zeta_{K}(s)=\zeta(s)L_{-4}(s)
 
\zeta_{K}(s)=\zeta(s)L_{-4}(s)
−
$$
+
</math>
 
따라서
 
따라서
−
$$\zeta_K'(0)=\zeta'(0)L_{-4}(0)+\zeta(0)L_{-4}'(0)$$
+
:<math>\zeta_K'(0)=\zeta'(0)L_{-4}(0)+\zeta(0)L_{-4}'(0)</math>
 
[[모든 자연수의 곱과 리만제타함수]]에 따르면,
 
[[모든 자연수의 곱과 리만제타함수]]에 따르면,
−
$$
+
:<math>
 
\begin{aligned}
 
\begin{aligned}
 
\zeta(0)&=-1/2\\
 
\zeta(0)&=-1/2\\
 
\zeta'(0)&=-\log \sqrt{2\pi}
 
\zeta'(0)&=-\log \sqrt{2\pi}
 
\end{aligned}
 
\end{aligned}
−
$$
+
</math>
  
 
한편, [[디리클레 L-함수의 미분]]에서 다음을 얻었다
 
한편, [[디리클레 L-함수의 미분]]에서 다음을 얻었다
−
$$
+
:<math>
 
\begin{aligned}
 
\begin{aligned}
 
L_{-4}(0)&=\frac{1}{2}\\
 
L_{-4}(0)&=\frac{1}{2}\\
 
L_{-4}'(0)&=-\log2+\log\frac{\Gamma(1/4)}{\Gamma(3/4)}=-\log2+\log \frac{\Gamma(1/4)^2}{\sqrt{2}\pi}
 
L_{-4}'(0)&=-\log2+\log\frac{\Gamma(1/4)}{\Gamma(3/4)}=-\log2+\log \frac{\Gamma(1/4)^2}{\sqrt{2}\pi}
 
\end{aligned}
 
\end{aligned}
−
$$
+
</math>
 
■
 
■
  
48번째 줄: 48번째 줄:
 
:<math>\frac{\pi }{\omega}=1.1981402347\cdots</math>
 
:<math>\frac{\pi }{\omega}=1.1981402347\cdots</math>
 
[[파일:렘니스케이트(lemniscate) 곡선의 길이와 타원적분2.png]]
 
[[파일:렘니스케이트(lemniscate) 곡선의 길이와 타원적분2.png]]
−
* 가우스는 이 수가 $\sqrt{2}$과 1의 [[산술 기하 평균 (arithmetic-geometric mean)]]이 되는 것을 관찰
+
* 가우스는 이 수가 <math>\sqrt{2}</math>과 1의 [[산술 기하 평균 (arithmetic-geometric mean)]]이 되는 것을 관찰
  
  
54번째 줄: 54번째 줄:
 
다음이 성립한다
 
다음이 성립한다
 
:<math>\frac{\pi }{\omega}=M(1,\sqrt2)</math>
 
:<math>\frac{\pi }{\omega}=M(1,\sqrt2)</math>
−
여기서 <math>M(a,b)</math> 은 두 수 $a, b$의 [[산술 기하 평균 (arithmetic-geometric mean)]]
+
여기서 <math>M(a,b)</math> 은 두 수 <math>a, b</math>의 [[산술 기하 평균 (arithmetic-geometric mean)]]
  
 
;증명
 
;증명
  
 
렘니스케이트 상수의 타원적분 표현
 
렘니스케이트 상수의 타원적분 표현
−
$$\frac{\omega}{2}=\frac{1}{\sqrt{2}}K(\frac{1}{\sqrt2})\label{ome}$$
+
:<math>\frac{\omega}{2}=\frac{1}{\sqrt{2}}K(\frac{1}{\sqrt2})\label{ome}</math>
 
한편 [[란덴변환(Landen's transformation)]] 에서 다음을 얻었다
 
한편 [[란덴변환(Landen's transformation)]] 에서 다음을 얻었다
−
$$K(\frac{1}{\sqrt2})=\frac{\pi}{2M(1,\frac{1}{\sqrt2})}\label{landen}$$
+
:<math>K(\frac{1}{\sqrt2})=\frac{\pi}{2M(1,\frac{1}{\sqrt2})}\label{landen}</math>
 
\ref{ome}와 \ref{landen}를 이용하여 다음을 얻는다:
 
\ref{ome}와 \ref{landen}를 이용하여 다음을 얻는다:
−
$$\frac{\pi}{\omega}=\frac{2K(\frac{1}{\sqrt2}){M(1,\frac{1}{\sqrt2})}}{\sqrt{2}K(\frac{1}{\sqrt2})} = \sqrt{2}M(1,\frac{1}{\sqrt2})=M(1,\sqrt2)$$
+
:<math>\frac{\pi}{\omega}=\frac{2K(\frac{1}{\sqrt2}){M(1,\frac{1}{\sqrt2})}}{\sqrt{2}K(\frac{1}{\sqrt2})} = \sqrt{2}M(1,\frac{1}{\sqrt2})=M(1,\sqrt2)</math>
 
■  
 
■  
 
===테이블===
 
===테이블===
−
$$
+
:<math>
 
\begin{array}{ccc}
 
\begin{array}{ccc}
 
  {n} & a_n & b_n \\
 
  {n} & a_n & b_n \\
81번째 줄: 81번째 줄:
 
  9 & 1.1981402347355922074 & 1.1981402347355922074 \\
 
  9 & 1.1981402347355922074 & 1.1981402347355922074 \\
 
\end{array}
 
\end{array}
−
$$
+
</math>
  
 
==급수 표현==
 
==급수 표현==
−
* [[아이젠슈타인 급수(Eisenstein series)]] $E_4$에 대하여 다음이 성립
+
* [[아이젠슈타인 급수(Eisenstein series)]] <math>E_4</math>에 대하여 다음이 성립
−
$$
+
:<math>
 
E_4(i)=3\left(\frac{\omega}{\pi}\right)^4=\frac{3\Gamma(\frac{1}{4})^8}{64 \pi ^{6}}
 
E_4(i)=3\left(\frac{\omega}{\pi}\right)^4=\frac{3\Gamma(\frac{1}{4})^8}{64 \pi ^{6}}
−
$$
+
</math>
 
* 다음과 같이 쓸 수 있다
 
* 다음과 같이 쓸 수 있다
−
$$
+
:<math>
−
\sum_{ (m,n) \neq (0,0)} \frac{1}{(mi+n)^{4}}=\frac{\omega^4}{15}
+
\sum_{ (m,n)\in \mathbb{Z}^2\backslash\{(0,0)\}} \frac{1}{(mi+n)^{4}}=\frac{\omega^4}{15}
−
$$
+
</math>
 +
* 다음이 성립한다
 +
:<math>
 +
\sum_{ (m,n)\in \mathbb{Z}^2\backslash\{(0,0)\}} \frac{1}{(mi+n)^{4s}}=G_{4s}\omega^{4s},\,s=1,2,\cdots
 +
</math>
 +
여기서 <math>G_{s}</math>는 다음과 같은 상수
 +
:<math>
 +
\begin{array}{c|cccccccc}
 +
s & 4 & 8 & 12 & 16 & 20 & 24 & 28 & 32 \\
 +
\hline
 +
G_s & \frac{1}{15} & \frac{1}{525} & \frac{2}{53625} & \frac{1}{1243125} & \frac{2}{118096875} & \frac{2}{5575415625} & \frac{4}{527240390625} & \frac{223}{1389278429296875} \\
 +
\end{array}
 +
</math>
 +
* <math>G_s</math>는 [[후르비츠 수 (Hurwitz number)]]의 예이다
  
 
==역사==
 
==역사==
120번째 줄: 133번째 줄:
  
 
   
 
   
−
 
+
[[분류:정수론]]
 
[[분류:원주율]]
 
[[분류:원주율]]
 
[[분류:상수]]
 
[[분류:상수]]
 +
 +
==메타데이터==
 +
===위키데이터===
 +
* ID :  [https://www.wikidata.org/wiki/Q6722 Q6722]
 +
===Spacy 패턴 목록===
 +
* [{'LOWER': 'carl'}, {'LOWER': 'friedrich'}, {'LEMMA': 'Gauss'}]
 +
* [{'LEMMA': 'Gauss'}]
 +
* [{'LOWER': 'johann'}, {'LOWER': 'carl'}, {'LOWER': 'friedrich'}, {'LEMMA': 'Gauss'}]
 +
* [{'LOWER': 'karl'}, {'LEMMA': 'Gauss'}]
 +
* [{'LOWER': 'c.'}, {'LOWER': 'f.'}, {'LEMMA': 'Gauss'}]
 +
* [{'LOWER': 'carl'}, {'LOWER': 'friedrich'}, {'LEMMA': 'Gauß'}]
 +
* [{'LOWER': 'gauß'}, {'OP': '*'}, {'LOWER': 'carl'}, {'LEMMA': 'Friedrich'}]

2021년 2월 17일 (수) 02:18 기준 최신판

개요

  • 렘니스케이트 상수 \(\omega\)를 다음과 같이 정의

\[\omega:=2\int_0^1\frac{dx}{\sqrt{1-x^4}}=2.622057554292\cdots\]

  • 다음과 같이 쓸 수 있다

\[ 2\omega=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}} \] 여기서 \(B\)는 오일러 베타적분(베타함수)이고, \(\Gamma\)는 감마함수


데데킨트 제타함수의 미분

정리

\[ \zeta_K'(0)=-\frac{1}{4}\log\left(\frac{\Gamma(\frac{1}{4})^4}{4\pi}\right)=-\frac{1}{4}\log 2\omega^2 \]

증명

이차 수체의 데데킨트 제타함수에서 \(\zeta_K(s)\)는 다음과 같이 분해됨을 보였다 \[ \zeta_{K}(s)=\zeta(s)L_{-4}(s) \] 따라서 \[\zeta_K'(0)=\zeta'(0)L_{-4}(0)+\zeta(0)L_{-4}'(0)\] 모든 자연수의 곱과 리만제타함수에 따르면, \[ \begin{aligned} \zeta(0)&=-1/2\\ \zeta'(0)&=-\log \sqrt{2\pi} \end{aligned} \]

한편, 디리클레 L-함수의 미분에서 다음을 얻었다 \[ \begin{aligned} L_{-4}(0)&=\frac{1}{2}\\ L_{-4}'(0)&=-\log2+\log\frac{\Gamma(1/4)}{\Gamma(3/4)}=-\log2+\log \frac{\Gamma(1/4)^2}{\sqrt{2}\pi} \end{aligned} \] ■


원주율과의 비교

  • 가우스는 단위원의 둘레의 길이와 렘니스케이트의 둘레의 길이의 비율을 계산하였다

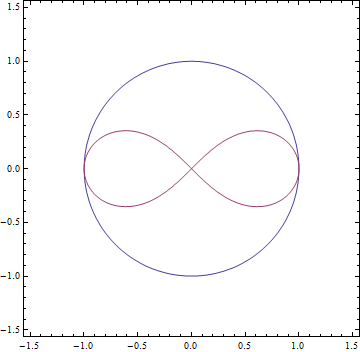
\[\pi=2\int_0^1\frac{dx}{\sqrt{1-x^2}}=3.14\cdots\] \[\omega=2\int_0^1\frac{dx}{\sqrt{1-x^4}}=2.62\cdots\] \[\frac{\pi }{\omega}=1.1981402347\cdots\] 렘니스케이트(lemniscate) 곡선의 길이와 타원적분2.png


정리

다음이 성립한다 \[\frac{\pi }{\omega}=M(1,\sqrt2)\] 여기서 \(M(a,b)\) 은 두 수 \(a, b\)의 산술 기하 평균 (arithmetic-geometric mean)

증명

렘니스케이트 상수의 타원적분 표현 \[\frac{\omega}{2}=\frac{1}{\sqrt{2}}K(\frac{1}{\sqrt2})\label{ome}\] 한편 란덴변환(Landen's transformation) 에서 다음을 얻었다 \[K(\frac{1}{\sqrt2})=\frac{\pi}{2M(1,\frac{1}{\sqrt2})}\label{landen}\] \ref{ome}와 \ref{landen}를 이용하여 다음을 얻는다: \[\frac{\pi}{\omega}=\frac{2K(\frac{1}{\sqrt2}){M(1,\frac{1}{\sqrt2})}}{\sqrt{2}K(\frac{1}{\sqrt2})} = \sqrt{2}M(1,\frac{1}{\sqrt2})=M(1,\sqrt2)\] ■

테이블

\[ \begin{array}{ccc} {n} & a_n & b_n \\ \hline 0 & 1.4142135623730950488 & 1.0000000000000000000 \\ 1 & 1.2071067811865475244 & 1.1892071150027210667 \\ 2 & 1.1981569480946342956 & 1.1981235214931201226 \\ 3 & 1.1981402347938772091 & 1.1981402346773072058 \\ 4 & 1.1981402347355922074 & 1.1981402347355922074 \\ 5 & 1.1981402347355922074 & 1.1981402347355922074 \\ 6 & 1.1981402347355922074 & 1.1981402347355922074 \\ 7 & 1.1981402347355922074 & 1.1981402347355922074 \\ 8 & 1.1981402347355922074 & 1.1981402347355922074 \\ 9 & 1.1981402347355922074 & 1.1981402347355922074 \\ \end{array} \]

급수 표현

\[ E_4(i)=3\left(\frac{\omega}{\pi}\right)^4=\frac{3\Gamma(\frac{1}{4})^8}{64 \pi ^{6}} \]

  • 다음과 같이 쓸 수 있다

\[ \sum_{ (m,n)\in \mathbb{Z}^2\backslash\{(0,0)\}} \frac{1}{(mi+n)^{4}}=\frac{\omega^4}{15} \]

  • 다음이 성립한다

\[ \sum_{ (m,n)\in \mathbb{Z}^2\backslash\{(0,0)\}} \frac{1}{(mi+n)^{4s}}=G_{4s}\omega^{4s},\,s=1,2,\cdots \] 여기서 \(G_{s}\)는 다음과 같은 상수 \[ \begin{array}{c|cccccccc} s & 4 & 8 & 12 & 16 & 20 & 24 & 28 & 32 \\ \hline G_s & \frac{1}{15} & \frac{1}{525} & \frac{2}{53625} & \frac{1}{1243125} & \frac{2}{118096875} & \frac{2}{5575415625} & \frac{4}{527240390625} & \frac{223}{1389278429296875} \\ \end{array} \]

역사

  • 1798~1799년의 시기에 가우스는 이 곡선의 길이와 관련하여 다음과 같은 기록을 일기에 남김. (Pi-unleashed, 99p)

We have gained some very elegant details about the lemniscate, which have exceeded all expectations, and indeed using methods which open up an entirely new field. That the AGM is equal to \(\frac{\pi }{\omega}\) between 1 and \(\sqrt{2}\) we have confirmed up to the 11th decimal digit; if this is proven, then a truly new field of analysis stands before us.


관련된 항목들


매스매티카 파일 및 계산 리소스

사전 형태의 자료

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'carl'}, {'LOWER': 'friedrich'}, {'LEMMA': 'Gauss'}]
  • [{'LEMMA': 'Gauss'}]
  • [{'LOWER': 'johann'}, {'LOWER': 'carl'}, {'LOWER': 'friedrich'}, {'LEMMA': 'Gauss'}]
  • [{'LOWER': 'karl'}, {'LEMMA': 'Gauss'}]
  • [{'LOWER': 'c.'}, {'LOWER': 'f.'}, {'LEMMA': 'Gauss'}]
  • [{'LOWER': 'carl'}, {'LOWER': 'friedrich'}, {'LEMMA': 'Gauß'}]
  • [{'LOWER': 'gauß'}, {'OP': '*'}, {'LOWER': 'carl'}, {'LEMMA': 'Friedrich'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=가우스의_렘니스케이트_상수&oldid=51967"