가우스의 렘니스케이트 상수

개요

렘니스케이트 상수 $\omega$를 다음과 같이 정의

\[\omega:=2\int_0^1\frac{dx}{\sqrt{1-x^4}}=2.622057554292\cdots\]

다음과 같이 쓸 수 있다

$$ 2\omega=B(1/2,1/4)=\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}=\frac{\Gamma(1/4)^2}{\sqrt{2\pi}} $$ 여기서 $B$는 오일러 베타적분(베타함수)이고, $\Gamma$는 감마함수

렘니스케이트 곡선의 둘레의 길이의 절반에 해당
타원곡선 y²=x³-x의 주기(periods)이며 초월수임

데데킨트 제타함수의 미분

수체 $K=\mathbb{Q}(\sqrt{-1})$의 데데킨트 제타함수

정리

$$ \zeta_K'(0)=-\frac{1}{4}\log\left(\frac{\Gamma(\frac{1}{4})^4}{4\pi}\right)=-\frac{1}{4}\log 2\omega^2 $$

증명

이차 수체의 데데킨트 제타함수에서 $\zeta_K(s)$는 다음과 같이 분해됨을 보였다 $$ \zeta_{K}(s)=\zeta(s)L_{-4}(s) $$ 따라서 $$\zeta_K'(0)=\zeta'(0)L_{-4}(0)+\zeta(0)L_{-4}'(0)$$ 모든 자연수의 곱과 리만제타함수에 따르면, $$ \begin{aligned} \zeta(0)&=-1/2\\ \zeta'(0)&=-\log \sqrt{2\pi} \end{aligned} $$

한편, 디리클레 L-함수의 미분에서 다음을 얻었다 $$ \begin{aligned} L_{-4}(0)&=\frac{1}{2}\\ L_{-4}'(0)&=-\log2+\log\frac{\Gamma(1/4)}{\Gamma(3/4)}=-\log2+\log \frac{\Gamma(1/4)^2}{\sqrt{2}\pi} \end{aligned} $$ ■

원주율과의 비교

가우스는 단위원의 둘레의 길이와 렘니스케이트의 둘레의 길이의 비율을 계산하였다

\[\pi=2\int_0^1\frac{dx}{\sqrt{1-x^2}}=3.14\cdots\] \[\omega=\int_0^1\frac{dx}{\sqrt{1-x^4}}=2.62\cdots\] \[\frac{\pi }{\omega}=1.1981402347\cdots\]

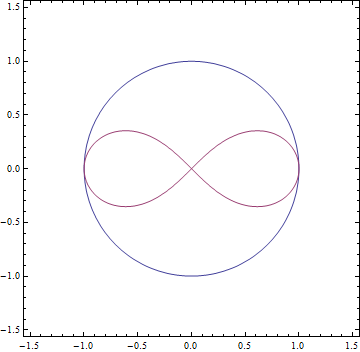
가우스는 이 수가 $\sqrt{2}$과 1의 산술 기하 평균 (arithmetic-geometric mean)이 되는 것을 관찰

정리

다음이 성립한다 \[\frac{\pi }{\omega}=M(1,\sqrt2)\] 여기서 $M(a,b)$ 은 두 수 $a, b$의 산술 기하 평균 (arithmetic-geometric mean)

증명

렘니스케이트 상수의 타원적분 표현 $$\frac{\omega}{2}=\frac{1}{\sqrt{2}}K(\frac{1}{\sqrt2})\label{ome}$$ 한편 란덴변환(Landen's transformation) 에서 다음을 얻었다 $$K(\frac{1}{\sqrt2})=\frac{\pi}{2M(1,\frac{1}{\sqrt2})}\label{landen}$$ \ref{ome}와 \ref{landen}를 이용하여 다음을 얻는다: $$\frac{\pi}{\omega}=\frac{2K(\frac{1}{\sqrt2}){M(1,\frac{1}{\sqrt2})}}{\sqrt{2}K(\frac{1}{\sqrt2})} = \sqrt{2}M(1,\frac{1}{\sqrt2})=M(1,\sqrt2)$$ ■

테이블

$$ \begin{array}{ccc} {n} & a_n & b_n \\ \hline 0 & 1.4142135623730950488 & 1.0000000000000000000 \\ 1 & 1.2071067811865475244 & 1.1892071150027210667 \\ 2 & 1.1981569480946342956 & 1.1981235214931201226 \\ 3 & 1.1981402347938772091 & 1.1981402346773072058 \\ 4 & 1.1981402347355922074 & 1.1981402347355922074 \\ 5 & 1.1981402347355922074 & 1.1981402347355922074 \\ 6 & 1.1981402347355922074 & 1.1981402347355922074 \\ 7 & 1.1981402347355922074 & 1.1981402347355922074 \\ 8 & 1.1981402347355922074 & 1.1981402347355922074 \\ 9 & 1.1981402347355922074 & 1.1981402347355922074 \\ \end{array} $$

급수 표현

아이젠슈타인 급수(Eisenstein series) $E_4$에 대하여 다음이 성립

$$ E_4(i)=3\left(\frac{\omega}{\pi}\right)^4=\frac{3\Gamma(\frac{1}{4})^8}{64 \pi ^{6}} $$

다음과 같이 쓸 수 있다

$$ \sum_{ (m,n) \neq (0,0)} \frac{1}{(mi+n)^{4}}=\frac{\omega^4}{15} $$

역사

1798~1799년의 시기에 가우스는 이 곡선의 길이와 관련하여 다음과 같은 기록을 일기에 남김. (Pi-unleashed, 99p)

We have gained some very elegant details about the lemniscate, which have exceeded all expectations, and indeed using methods which open up an entirely new field. That the AGM is equal to $\frac{\pi }{\omega}$ between 1 and $\sqrt{2}$ we have confirmed up to the 11th decimal digit; if this is proven, then a truly new field of analysis stands before us.

매스매티카 파일 및 계산 리소스

사전 형태의 자료

http://en.wikipedia.org/wiki/Gauss's_constant