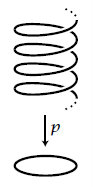|
|
| (사용자 2명의 중간 판 17개는 보이지 않습니다) |
| 1번째 줄: |
1번째 줄: |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">이 항목의 스프링노트 원문주소</h5>
| + | ==개요== |
| | | | |
| − | * [[복소로그함수]]<br> | + | * [[로그 함수]]의 복소수로의 확장 |
| | | | |
| − |
| + | |
| | | | |
| − |
| |
| | | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">개요</h5>
| + | |
| | | | |
| − | * [[로그 함수|로그함수]]의 복소수로의 확장<br>
| + | ==복소로그함수== |
| | | | |
| − |
| + | 복소로그함수는 복소수 <math>z = re^{i\theta}</math> 에 대하여, 다음과 같이 정의된다 |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | <h5 style="margin: 0px; line-height: 2em;">복소로그함수</h5>
| |
| − | | |
| − | 복소로그함수는 복소수 <math>z = re^{i\theta}</math> 에 대하여, 다음과 같이 정의된다 | |
| | | | |
| | <math>\log(z) = \ln|z| + i\arg(z) = \ln(r) + i\left(\theta + 2 \pi k \right)</math>. 여기서 <math>k\in\mathbb{Z}</math>. | | <math>\log(z) = \ln|z| + i\arg(z) = \ln(r) + i\left(\theta + 2 \pi k \right)</math>. 여기서 <math>k\in\mathbb{Z}</math>. |
| 31번째 줄: |
22번째 줄: |
| | <math>\log(1)</math>의 값이 무한대로 많은 것이다. 뭔가 이상하다? | | <math>\log(1)</math>의 값이 무한대로 많은 것이다. 뭔가 이상하다? |
| | | | |
| − |
| + | |
| | | | |
| − | 중고등학교에서 '함수'의 개념을 가르칠때, 가장 강조되는 것은 함수는 각 정의역의 원소에 대하여, 공역의 원소가 하나씩 대응되어야 한다는 것이다. 그러니 이대로는 복소로그함수는 함수가 아니다! | + | 중고등학교에서 '함수'의 개념을 가르칠 때, 가장 강조되는 것은 함수는 각 정의역의 원소에 대하여, 공역의 원소가 하나씩 대응되어야 한다는 것이다. 그러니 이대로는 복소로그함수는 함수가 아니다! |
| | | | |
| | 학부의 복소함수론에서는 이러한 상황을 타개하기 위하여 복소평면에서 원점에서 시작되는 반직선을 뺀 영역에서 복소로그함수를 정의하며 그 '''공역, 즉 함수값이 가질 수 있는 영역을 제한'''하는 것이 보통이다. | | 학부의 복소함수론에서는 이러한 상황을 타개하기 위하여 복소평면에서 원점에서 시작되는 반직선을 뺀 영역에서 복소로그함수를 정의하며 그 '''공역, 즉 함수값이 가질 수 있는 영역을 제한'''하는 것이 보통이다. |
| 39번째 줄: |
30번째 줄: |
| | 그러나 이러한 방식으로는 이 함수를 어떻게 이해하는 것이 정말로 올바른 것인지 제대로 답할 수 없다. | | 그러나 이러한 방식으로는 이 함수를 어떻게 이해하는 것이 정말로 올바른 것인지 제대로 답할 수 없다. |
| | | | |
| − |
| + | |
| | | | |
| | 문제의 원인을 잘 들여다보면, 이것은 [[원 위에서 각도함수 정의하기|원위의 점에 정의되는 각도함수]]를 정의하는 것이 불가능한 이유와 같음을 알 수 있다. 각도함수라는 것을 정의할 수 있는 곳은 원이 아니라, 원 위에 놓여 나선처럼 놓인 직선이었다. | | 문제의 원인을 잘 들여다보면, 이것은 [[원 위에서 각도함수 정의하기|원위의 점에 정의되는 각도함수]]를 정의하는 것이 불가능한 이유와 같음을 알 수 있다. 각도함수라는 것을 정의할 수 있는 곳은 원이 아니라, 원 위에 놓여 나선처럼 놓인 직선이었다. |
| | | | |
| − | [http://lh5.ggpht.com/_knry6PkLCS4/SbmZwU-6zkI/AAAAAAAAXrU/IzZXmtQmVSo/s800/%EC%A0%84%EC%B2%B4%ED%99%94%EB%A9%B4%20%EC%BA%A1%EC%B2%98%202009-03-12%20%EC%98%A4%ED%9B%84%2042318.jpg ] | + | [[파일:Covering.jpg]] |
| − | | |
| − |
| |
| | | | |
| | 이 상황을 정리하기 위해서는 이와 같은 발상의 전환이 필요하다. 그것은 ''''공역'을 제한하는 것이 아니라 바로 '정의역'을 바꾸는 것'''이다. 로그함수는 원점을 제외한 복소평면에서 정의되는 함수가 아니다. | | 이 상황을 정리하기 위해서는 이와 같은 발상의 전환이 필요하다. 그것은 ''''공역'을 제한하는 것이 아니라 바로 '정의역'을 바꾸는 것'''이다. 로그함수는 원점을 제외한 복소평면에서 정의되는 함수가 아니다. |
| 55번째 줄: |
44번째 줄: |
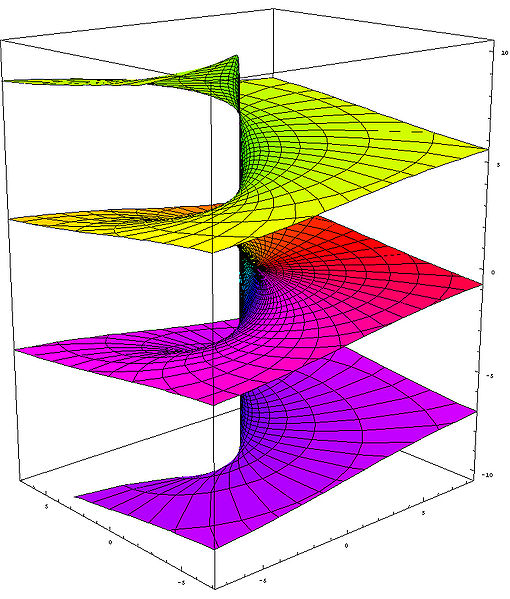
| | 위의 원과 그 위에 놓인 나선(결국은 직선) 의 관계처럼, 원점을 뺀 복소평면을 나선처럼 감고 올라가는 곡면을 복소로그함수의 올바른 정의역으로 보아야 한다. | | 위의 원과 그 위에 놓인 나선(결국은 직선) 의 관계처럼, 원점을 뺀 복소평면을 나선처럼 감고 올라가는 곡면을 복소로그함수의 올바른 정의역으로 보아야 한다. |
| | | | |
| − | 1 이라는 복소수를 이 곡면의 한 점으로 볼 것이 아니라, 그냥 1이 있다면, 1에서 시작해서 원점 주변을 한바퀴 돌고 돌아온 또다른 1, 두바퀴 돌때 생기는 1, ... 이렇게 본래의 복소평면에 있는 1에 대응되는 수많은 새로운 1이라는 점들이 이 곡면에 놓여 있는 것이다. 이 곡면을 복소로그함수 <math>\log(z)</math>의 [http://en.wikipedia.org/wiki/Riemann_surface 리만곡면]이라고 부른다. | + | 1 이라는 복소수를 이 곡면의 한 점으로 볼 것이 아니라, 그냥 1이 있다면, 1에서 시작해서 원점 주변을 한바퀴 돌고 돌아온 또다른 1, 두바퀴 돌때 생기는 1, ... 이렇게 본래의 복소평면에 있는 1에 대응되는 수많은 새로운 1이라는 점들이 이 곡면에 놓여 있는 것이다. 이 곡면을 복소로그함수 <math>\log(z)</math>의 [http://en.wikipedia.org/wiki/Riemann_surface 리만곡면]이라고 부른다. |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | [[Media:|]]
| |
| − | | |
| − |
| |
| − | | |
| − | 복소로그함수가 사는 곳은 복소평면이 아니라 바로 이렇게 무한히 펼쳐지는 곡면이다.
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | <h5 style="margin: 0px; line-height: 2em;">로그함수와 맴돌이</h5>
| |
| − | | |
| − |
| |
| − | | |
| − | 로그함수를 이해하는 또다른 관점에 대하여 생각해 보려 한다.
| |
| − | | |
| − |
| |
| − | | |
| − | 복소함수 <math>y(z)</math>에 대한 [[오일러 미분방정식]] 을 생각해보자.
| |
| − | | |
| − | <math>z^2\frac{d^2y}{dz^2}+\alpha z\frac{dy}{dz}+\beta y=0</math>
| |
| − | | |
| − | 이 미분방정식은 원점 즉, <math>z=0</math>에서 특이점을 가진다.
| |
| − | | |
| − |
| |
| − | | |
| − | 로그함수에 대하여 생각하고 있으므로, 특별히 <math>\alpha=1</math>, <math>\beta=0</math> 인 간단한 경우를 생각해 보자.
| |
| − | | |
| − | <math>z^2\frac{d^2y}{dz^2}+ z\frac{dy}{dz}=0</math>
| |
| − | | |
| − | 선형 [[이계 미분방정식]] 이므로 <math>z=1</math> 근방의 공간에서 두 개의 일차독립인 해가 존재한다.
| |
| − | | |
| − |
| |
| − | | |
| − | 두 함수 <math>y_1=1</math>과 <math>y_2=\log z</math> (국소적으로 생각하고 있으므로, <math>y_2(1)=0</math> 인 로그함수의 가지(branch)를 선택) 가 미분방정식의 <math>z=1</math> 근방에서의 해공간의 기저가 된다.
| |
| − | | |
| − | <math>y_1'=0</math>이므로 미분방정식의 해이다. 또, <math>y_2'=1/z</math>, <math>y_2''=-1/z^2</math>이므로 역시 미분방정식의 해이다.
| |
| − | | |
| − | 즉 이 미분방정식의 <math>z=1</math> 근방의 모든 해는 적당한 복소수 <math>c_1,c_2</math>에 대하여 <math>y(z)=c_1+c_2\log z=c_1y_1+c_2y_2</math>의 형태로 쓸 수 있다.
| |
| − | | |
| − |
| |
| − | | |
| − | 이제 이렇게 얻어진 미분방정식의 해를 가지고, 해석적확장을 할 때 생기는 현상에 대하여 생각해보자.
| |
| − | | |
| − | 1은 해석함수(analytic function)이므로, 어떤 경로를 따라서 움직이든 해석적확장(analytic continuation) 에 의해 변하지 않는다. 즉 원점 주위를 한바퀴 반시계방향으로 회전하며 해석적확장을 해도 <math>1 =1 \cdot y_1+0 \cdot y_2</math> 으로 남아 있다.
| |
| − | | |
| − | 한편, 미분방정식의 특이점인 <math>z=0</math> 즉, 원점 주위를 <math>z=1</math>에서 시작하여 한바퀴 반시계 방향으로 회전하며 <math>y_1=\log z</math>를 해석적으로 확장하여 같은 자리로 돌아오는 경우, [http://bomber0.byus.net/index.php/2010/01/23/1748 복소로그함수와 리만곡면]에서 보았듯이 <math>2\pi i</math>만큼 다른 값을 가지는 새로운 함수 <math>\log z+2\pi i=2\pi i\cdot y_1+1 \cdot y_2</math> 를 얻게 된다.
| |
| − | | |
| − |
| |
| − | | |
| − | 따라서 원점 주위를 반시계 방향으로 도는 닫힌 경로는, 이 경로를 따라가는 해석적확장 과정을 통해 해공간을 변화시키는 선형사상으로 이해할 경우, 미분방정식의 해공간의 기저 <math>y_1,y_2</math>에 대하여 행렬
| |
| − | | |
| − | <math>\begin{pmatrix} 1 & 2\pi i \\ 0 & 1 \end{pmatrix}</math>
| |
| − | | |
| − | 에 대응된다.
| |
| | | | |
| − |
| + | |
| | + | [[파일:Riemann surface log.jpg510px-Riemann surface log.jpg]] |
| | | | |
| − | 한바퀴 도는 경우가 행렬 <math>\begin{pmatrix} 1 & 2\pi i \\ 0 & 1 \end{pmatrix}</math>에 대응되므로, 두바퀴 도는 경우는 <math>\begin{pmatrix} 1 & 4\pi i \\ 0 & 1 \end{pmatrix}</math>, 세바퀴 도는 경우는 <math>\begin{pmatrix} 1 & 6\pi i \\ 0 & 1 \end{pmatrix}</math>, 거꾸로 한바퀴 도는 경우는 <math>\begin{pmatrix} 1 & -2\pi i \\ 0 & 1 \end{pmatrix}</math> ... 에 대응된다.
| + | 복소로그함수가 사는 곳은 복소평면이 아니라 바로 이렇게 무한히 펼쳐지는 곡면이다. |
| | | | |
| − |
| + | |
| | | | |
| − | 일반적으로 이렇게 특이점이 있는 미분방정식의 해를 특이점 주변에서 해석적확장을 하며 얻어지는 원점 주변에 놓인 닫힌 루프에 대응되는 행렬들, 즉 준동형사상(homomorphism) <math>\pi_1 \to \operatorname{GL}_2(\mathbb{C})</math> 를 미분방정식에 대한 맴돌이 표현(monodromy representation)이라 하며, 이 때의 치역(image)을 맴돌이군(monodromy group)이라 한다. 여기서 <math>\pi_1</math> 은 복소평면에서 특이점들을 뺀 공간의 fundamental group. 이러한 개념들을 이해해야, 히 ‘[http://en.wikipedia.org/wiki/Hilbert%27s_twenty-first_problem Proof of the Existence of Linear Differential Equations Having a Prescribed Monodromic Group]’ [http://en.wikipedia.org/wiki/Hilbert%27s_twenty-first_problem http://en.wikipedia.org/wiki/Hilbert’s_twenty-first_problem] 와 같은 수학에 접근할 수 있다.
| + | |
| | | | |
| − |
| + | |
| | | | |
| − | 즉 오일러 미분방정식의 특별한 경우인 <math>z^2\frac{d^2y}{dz^2}+ z\frac{dy}{dz}=0</math> 의 맴돌이군은 정수들이 이루는 군 <math>\mathbb{Z}</math>가 된다.
| + | ==로그함수와 맴돌이== |
| | + | * [[맴돌이군과 미분방정식]] |
| | | | |
| − |
| |
| | | | |
| − | 복소로그함수를 이해하려면 앞에서처럼 리만곡면에서 정의되는 함수로 이해하든지, 아니면 이렇게 미분방정식과 그 맴돌이군을 통해 이해하던지 그때그때 필요한대로 선택하면 된다.
| |
| | | | |
| − |
| |
| | | | |
| − |
| + | |
| − | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">역사</h5>
| |
| − | | |
| − |
| |
| | | | |
| | + | ==역사== |
| | * http://www.google.com/search?hl=en&tbs=tl:1&q= | | * http://www.google.com/search?hl=en&tbs=tl:1&q= |
| − | * [[수학사연표 (역사)|수학사연표]] | + | * [[수학사 연표]] |
| − | *
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| | | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">메모</h5>
| + | |
| | | | |
| − |
| + | |
| | | | |
| − |
| + | ==메모== |
| | + | * [http://bomber0.byus.net/index.php/2010/01/23/1748 복소로그함수와 리만곡면] |
| | | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">관련된 항목들</h5>
| + | |
| | | | |
| − | * [[로그 함수|로그함수]]<br> | + | ==관련된 항목들== |
| − | * [[대수적위상수학]]<br> | + | * [[로그 함수]] |
| − | * [[제1종타원적분 K (complete elliptic integral of the first kind)]]<br> | + | * [[대수적위상수학]] |
| | + | * [[제1종타원적분 K (complete elliptic integral of the first kind)]] |
| | | | |
| − |
| + | |
| | | | |
| − |
| |
| | | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">수학용어번역</h5>
| + | |
| | | | |
| − | * 단어사전 http://www.google.com/dictionary?langpair=en|ko&q=
| + | ==사전 형태의 자료== |
| − | * 발음사전 http://www.forvo.com/search/
| |
| − | * [http://mathnet.kaist.ac.kr/mathnet/math_list.php?mode=list&ftype=&fstr= 대한수학회 수학 학술 용어집]<br>
| |
| − | ** http://mathnet.kaist.ac.kr/mathnet/math_list.php?mode=list&ftype=eng_term&fstr=
| |
| − | * [http://www.nktech.net/science/term/term_l.jsp?l_mode=cate&s_code_cd=MA 남·북한수학용어비교]
| |
| − | * [http://kms.or.kr/home/kor/board/bulletin_list_subject.asp?bulletinid=%7BD6048897-56F9-43D7-8BB6-50B362D1243A%7D&boardname=%BC%F6%C7%D0%BF%EB%BE%EE%C5%E4%B7%D0%B9%E6&globalmenu=7&localmenu=4 대한수학회 수학용어한글화 게시판]
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">사전 형태의 자료</h5>
| |
| | | | |
| | * http://ko.wikipedia.org/wiki/ | | * http://ko.wikipedia.org/wiki/ |
| | * http://en.wikipedia.org/wiki/Complex_logarithm | | * http://en.wikipedia.org/wiki/Complex_logarithm |
| − | * http://en.wikipedia.org/wiki/
| + | [[분류:리만곡면론]] |
| − | * http://www.wolframalpha.com/input/?i=
| + | [[분류:복소함수론]] |
| − | * [http://dlmf.nist.gov/ NIST Digital Library of Mathematical Functions]
| |
| − | * [http://www.research.att.com/%7Enjas/sequences/index.html The On-Line Encyclopedia of Integer Sequences]<br>
| |
| − | ** http://www.research.att.com/~njas/sequences/?q=
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">관련논문</h5>
| |
| − | | |
| − | * http://www.jstor.org/action/doBasicSearch?Query=
| |
| − | * http://www.ams.org/mathscinet
| |
| − | * http://dx.doi.org/
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">관련도서</h5>
| |
| − | | |
| − | * 도서내검색<br>
| |
| − | ** http://books.google.com/books?q=
| |
| − | ** http://book.daum.net/search/contentSearch.do?query=
| |
| − | * 도서검색<br>
| |
| − | ** http://books.google.com/books?q=
| |
| − | ** http://book.daum.net/search/mainSearch.do?query=
| |
| − | ** http://book.daum.net/search/mainSearch.do?query=
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">관련기사</h5>
| |
| − | | |
| − | * 네이버 뉴스 검색 (키워드 수정)<br>
| |
| − | ** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
| |
| − | ** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
| |
| − | ** http://news.search.naver.com/search.naver?where=news&x=0&y=0&sm=tab_hty&query=
| |
| − | | |
| − |
| |
| − | | |
| − |
| |
| − | | |
| − | <h5 style="margin: 0px; line-height: 3.428em; color: rgb(34, 61, 103); font-family: 'malgun gothic',dotum,gulim,sans-serif; font-size: 1.166em; background-position: 0px 100%;">블로그</h5>
| |
| | | | |
| − | * 구글 블로그 검색<br>
| + | ==메타데이터== |
| − | ** http://blogsearch.google.com/blogsearch?q=
| + | ===위키데이터=== |
| − | * [http://navercast.naver.com/science/list 네이버 오늘의과학] | + | * ID : [https://www.wikidata.org/wiki/Q753035 Q753035] |
| − | * [http://math.dongascience.com/ 수학동아]
| + | ===Spacy 패턴 목록=== |
| − | * [http://www.ams.org/mathmoments/ Mathematical Moments from the AMS]
| + | * [{'LOWER': 'riemann'}, {'LEMMA': 'surface'}] |
| − | * [http://betterexplained.com/ BetterExplained] | |