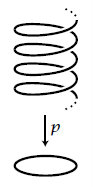원 위에서 각도함수 정의하기
개요
- 원점을 중심으로 하고, 반지름이 r 인 원 \(x^2 + y^2=r^2\) 위에서 각도함수를 연속적으로 확장하는 것은 불가능
- 각도함수는 원이 아닌 원의 보편 덮개 (universal covering) 에서 정의되는 함수이다
- 1-미분형식 \(d\theta\) 는 단위원 위에서 정의된다
\[d\theta = \frac{1}{r^2} \left( x\,dy - y\,dx \right)\]
- 이 미분형식은 각원소 벡터장이라는 이름으로 불리기도 한다
- 각도함수는 이 미분형식의 원 위에서의 선적분으로 표현된다
\[\theta =\int_C \,\frac{x\,dy-y\,dx}{x^2+y^2} \]
각도함수를 왜 연속함수로 확장할 수 없나
먼저 원위에서 한바퀴를 돌면 \(2\pi\) (라디안) 만큼의 각의 변화가 있다는 사실은 고딩 1학년 정도에서 배울 것입니다. 이에 대해서는 라디안 항목을 참고하시기 바랍니다.
단위원의 모든 점 (x,y)에서 연속적으로 정의된 각도함수 \(\theta\)의 값 \(\theta(P)\) 를 정의하는 일이 가능한지 생각해 봅시다.
일단 시작을 위해 점 (1,0)에 일단 각도함수의 값을 \(\theta(1,0)=0\) 이라고 정의를 해봅시다. 위의 그림대로 원위의 점을 따라 조금씩 반시계 방향으로 이동하면서 각도함수를 연속적으로 정의해 나갈수가 있을 것으로 보입니다. 하지만 문제는 원의 한바퀴를 돌아서 다시 같은 점에 돌아왔을 때 발생합니다. 이미 \(\theta(1,0)=0\) 으로 정의를 해놓은 마당에, 반시계 방향으로 원주 한바퀴를 돌면서 \(\theta(x,y)\)의 정의를 확장해 가다보면, 각도함수를 연속함수로 정의하기 위해서는 \(\theta(1,0)=2\pi\) 라고 정의를 해야하는 문제에 봉착하게 됩니다.
결론은 단위원의 모든 점 (x,y)에서 연속적으로 정의된 각도함수 \(\theta\)를 정의하는 것은 불가능하다는 것입니다. 그럼에도 우리는 연속적으로 계속 확장이 가능한 각도함수 \(\theta\) 를 잘 이해할 수 있을 것 같다는 듭니다. 이 문제를 어떻게 해결해야 할까요?
함수는 분명히 있는데, 정의역이 원이 아니다. 그렇다면 도대체 정의역이 무엇이란 말인가? 이 문제에 대해 생각을 하다보면, 우리는 원 위에 놓여 있는 또다른 기하학적 공간을 발견하게 됩니다. 이것은 다름 아닌 직선입니다.
학부수학의 뼈대 에서 보여드린 바로 그 그림인 것이지요.
원위에서 각도함수를 정의하려다, 우리는 그것이 불가능함을 알게 되었습니다. 원이라는 공간과 거기서 국소적으로 확장 가능한 함수가 만나, 우리는 원위에 펼쳐진 새로운 공간을 발견하게 됩니다. 결론적으로 각도함수가 정의되어 있는 '올바른' 공간은 원이 아니라, 원을 무한번 둘둘 감고 있는 '직선'을 발견하게 되는 것입니다.
universal covering
직선위의 한 점 즉 실수 \(\theta\) 에 대하여 대응되는 단위원 위의 한 점 \((\cos \theta,\sin \theta)\)은 크기가 1인 복소수 \(e^{i \theta}= \cos \theta + i \sin \theta\)로 이해할 수 있다.
따라서 \(\theta\)를 \(e^{i \theta}= \cos \theta + i \sin \theta\) 로 보내는 함수가 바로 아래 그림의 p이며,
각도라는 것은 원위의 한점 \(e^{i \theta}= \cos \theta + i \sin \theta\)에 대응되는 모든 실수 \(\theta\) \(\cdots, \theta-2\pi, \theta,\theta+2\pi,\cdots\) 가 되며,
각도함수란 실수 \(\theta\) 를 \(\theta\)로 보내는 함수로 이해할 수 있다.
메모
관련된 항목들
사전 형태의 자료
메타데이터
위키데이터
- ID : Q576728
Spacy 패턴 목록
- [{'LOWER': 'winding'}, {'LEMMA': 'number'}]