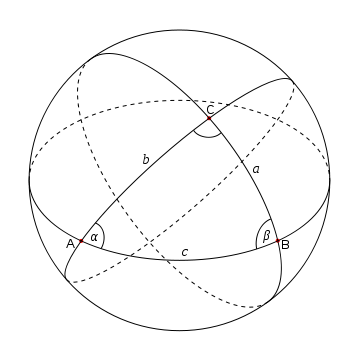
구면삼각법
둘러보기로 가기
검색하러 가기
개요
사인과 코사인 법칙
사인 법칙
\[ \frac{\sin A}{\sin a}=\frac{\sin B}{\sin b}=\frac{\sin C}{\sin c} \]
코사인 법칙
\[\cos a= \cos b \cos c + \sin b \sin c \cos A \!\] \[\cos b= \cos c \cos a + \sin c \sin a \cos B \!\] \[\cos c= \cos a \cos b + \sin a \sin b \cos C \!\]
직각삼각형
- \(C=\pi/2\)라 가정하는 경우, 네이피어의 공식을 얻는다
\( \begin{alignat}{4} &\text{(R1)}&\qquad \cos c&=\cos a\,\cos b, &\qquad\qquad &\text{(R6)}&\qquad \tan b&=\cos A\,\tan c,\\ &\text{(R2)}& \sin a&=\sin A\,\sin c, &&\text{(R7)}& \tan a&=\cos B\,\tan c,\\ &\text{(R3)}& \sin b&=\sin B\,\sin c, &&\text{(R8)}& \cos A&=\sin B\,\cos a,\\ &\text{(R4)}& \tan a&=\tan A\,\sin b, &&\text{(R9)}& \cos B&=\sin A\,\cos b,\\ &\text{(R5)}& \tan b&=\tan B\,\sin a, &&\text{(R10)}& \cos c&=\cot A\,\cot B. \end{alignat} \)
메모
- http://www.johndcook.com/spherical_trigonometry.html
- http://home.scarlet.be/~ping1339/boldriehoeks.htm
관련된 항목들
매스매티카 파일 및 계산 리소스
사전 형태의 자료
리뷰, 에세이, 강의노트
- UHG36: Classical Spherical Trigonometry. 2012. http://www.youtube.com/watch?v=hcXbLRPq5vc
메타데이터
위키데이터
- ID : Q46463
Spacy 패턴 목록
- [{'LOWER': 'spherical'}, {'LEMMA': 'trigonometry'}]