마르코프 체인
둘러보기로 가기
검색하러 가기
예
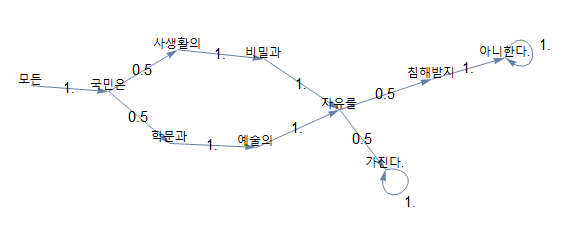
- 다음의 문장이 주어져 있다
- 모든 국민은 학문과 예술의 자유를 가진다.
- 모든 국민은 사생활의 비밀과 자유를 침해받지 아니한다.
- 두 문장에 나오는 단어들은 이 확률과정의 상태공간 S를 이룬다
- S={"모든", "국민은", "비밀과", "예술의", "자유를", "학문과", "가진다.", "사생활의", "침해받지", "아니한다."}
- "모든" 이라는 단어(상태)에서 출발하여, 연결된 선을 따라 다음 단어로 이동하며 (전이), 마침표가 있는 단어에 이르면 이 과정을 종료한다
- 한 단어에서 다음 단어로 넘어갈 확률은 두 단어가 연결된 빈도로부터 얻어진다
- 이러한 확률과정을 통하여, 새로운 문장을 생성할 수 있게 된다
- 예: "모든 국민은 학문과 예술의 자유를 침해받지 아니한다"
- 이는 현재의 한 단어만이 다음 단어에 영향을 주는 '바이그램' 모형이다
관련된 항목들
매스매티카 파일
노트
위키데이터
- ID : Q176645
말뭉치
- Markov chains, named after Andrey Markov, are mathematical systems that hop from one "state" (a situation or set of values) to another.[1]
- Of course, real modelers don't always draw out Markov chain diagrams.[1]
- This means the number of cells grows quadratically as we add states to our Markov chain.[1]
- One use of Markov chains is to include real-world phenomena in computer simulations.[1]
- Markov chain analysis is concerned in general with how long individual entities spend, on average, in different states before being absorbed and on first passage times to absorbing states.[2]
- Thus Markov chain analysis is ideal for providing insights on life history or anything related to timing.[2]
- Life expectancy – The fundamental matrix in Markov chain analysis provides a measure of expected time in each state before being absorbed.[2]
- Markov chains are a fairly common, and relatively simple, way to statistically model random processes.[3]
- A popular example is r/SubredditSimulator, which uses Markov chains to automate the creation of content for an entire subreddit.[3]
- Overall, Markov Chains are conceptually quite intuitive, and are very accessible in that they can be implemented without the use of any advanced statistical or mathematical concepts.[3]
- This example illustrates many of the key concepts of a Markov chain.[3]
- A (time-homogeneous) Markov chain built on states A and B is depicted in the diagram below.[4]
- If the Markov chain in Figure 21.3 is used to model time-varying propagation loss, then each state in the chain corresponds to a different loss.[5]
- Each number represents the probability of the Markov process changing from one state to another state, with the direction indicated by the arrow.[6]
- A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC).[6]
- A continuous-time process is called a continuous-time Markov chain (CTMC).[6]
- However, many applications of Markov chains employ finite or countably infinite state spaces, which have a more straightforward statistical analysis.[6]
- His analysis did not alter the understanding or appreciation of Pushkin’s poem, but the technique he developed—now known as a Markov chain—extended the theory of probability in a new direction.[7]
- In physics the Markov chain simulates the collective behavior of systems made up of many interacting particles, such as the electrons in a solid.[7]
- And Markov chains themselves have become a lively area of inquiry in recent decades, with efforts to understand why some of them work so efficiently—and some don’t.[7]
- As Markov chains have become commonplace tools, the story of their origin has largely faded from memory.[7]
- A Markov chain describes the transitions between a given set of states using transition probabilities.[8]
- A Markov chain evolves in discrete time and moves step by step from state to state; the step size can be chosen arbitrarily, and depending on the application, it could be 1 day, or 1 month, or 1 year.[8]
- Transition probabilities only depend on the current state the Markov chain is in at time t, and not on any previous states at t−1,t−2, ….[8]
- Markov chains are usually analyzed in matrix notation.[8]
- But the concept of modeling sequences of random events using states and transitions between states became known as a Markov chain.[9]
- One of the first and most famous applications of Markov chains was published by Claude Shannon.[9]
- For a Markov chain to be ergodic, two technical conditions are required of its states and the non-zero transition probabilities; these conditions are known as irreducibility and aperiodicity.[10]
- It follows from Theorem 21.2.1 that the random walk with teleporting results in a unique distribution of steady-state probabilities over the states of the induced Markov chain.[10]
- In the improved multivariate Markov chain model, Ching et al. incorporated positive and negative association parts.[11]
- With the developments of Markov chain models and their applications, the number of the sequences may be larger.[11]
- It is inevitable that a large categorical data sequence group will cause high computational cost in multivariate Markov chain model.[11]
- In Section 2, we review two lemmas and several Markov chain models.[11]
- The Season 1 episode "Man Hunt" (2005) of the television crime drama NUMB3RS features Markov chains.[12]
- Along the way, you are welcome to talk with other students (don't forget we have a Blackboard Q&A discussion forum!) and explore how others have used Markov chains.[13]
- A Markov chain is a mathematical model that describes movement (transitions) from one state to another.[13]
- In a first-order Markov chain, this probability only depends on the current state, and not any further transition history.[13]
- We can build more "memory" into our model by using a higher-order Markov chain.[13]
- The paper also investigates the definition of stochastic monotonicity on a more general state space, and the properties of integer-valued stochastically monotone Markov Chains.[14]
- Markov chain Monte Carlo using the Metropolis-Hastings algorithm is a general method for the simulation of stochastic processes having probability densities known up to a constant of proportionality.[15]
- Consider the problem of modelling memory effects in discrete-state random walks using higher-order Markov chains.[16]
- As an illustration of model selection for multistep Markov chains, this manuscript re-examines the hot hand phenomenon from a different analytical philosophy.[16]
- The memoryless property of Markov chains refers to h = 1.[16]
- This manuscript addressed general methods of degree selection for multistep Markov chain models.[16]
- A Markov chain is a mathematical system usually defined as a collection of random variables, that transition from one state to another according to certain probabilistic rules.[17]
- The algorithm known as PageRank, which was originally proposed for the internet search engine Google, is based on a Markov process.[17]
- A discrete-time Markov chain involves a system which is in a certain state at each step, with the state changing randomly between steps.[17]
- A Markov chain is represented using a probabilistic automaton (It only sounds complicated!).[17]
- This unique guide to Markov chains approaches the subject along the four convergent lines of mathematics, implementation, simulation, and experimentation.[18]
- An introduction to simple stochastic matrices and transition probabilities is followed by a simulation of a two-state Markov chain.[18]
- The notion of steady state is explored in connection with the long-run distribution behavior of the Markov chain.[18]
- Predictions based on Markov chains with more than two states are examined, followed by a discussion of the notion of absorbing Markov chains.[18]
- We next give examples that illustrate various properties of quantum Markov chains.[19]
- First, the probability sequence is treated as consisting of successive realizations of a stochastic process, and the stochastic process is modeled using Markov chain theory.[20]
- The size and stationarity of the reforecast ensemble dataset permits straightforward estimation of the parameters of certain Markov chain models.[20]
- Finally, opportunities to apply the Markov chain model to decision support are highlighted.[20]
- In this same framework, the importance of recognizing inhomogeneity in the Markov chain parameters when specifying decision intervals is illustrated.[20]
- The extra questions are interesting and off the well-beaten path of questions that are typical for an introductory Markov Chains course.[21]
- CUP 1997 (Chapter 1, Discrete Markov Chains is freely available to download.[21]
- (Each of these books contains a readable chapter on Markov chains and many nice examples.[21]
- See also, Sheldon Ross and Erol Pekoz, A Second Course in Probability, 2007 (Chapter 5 gives a readable treatment of Markov chains and covers many of the topics in our course.[21]
- Markov chains are used to model probabilities using information that can be encoded in the current state.[22]
- More technically, information is put into a matrix and a vector - also called a column matrix - and with many iterations, a collection of probability vectors makes up Markov chains.[22]
- Representing a Markov chain as a matrix allows for calculations to be performed in a convenient manner.[22]
- A Markov chain is one example of a Markov model, but other examples exist.[22]
- So far, we have discussed discrete-time Markov chains in which the chain jumps from the current state to the next state after one unit time.[23]
- Markov chain Monte Carlo is one of our best tools in the desperate struggle against high-dimensional probabilistic computation, but its fragility makes it dangerous to wield without adequate training.[24]
- Unfortunately the Markov chain Monte Carlo literature provides limited guidance for practical risk management.[24]
- Before introducing Markov chain Monte Carlo we will begin with a short review of the Monte Carlo method.[24]
- Finally we will discuss how these theoretical concepts manifest in practice and carefully study the behavior of an explicit implementation of Markov chain Monte Carlo.[24]
소스
- ↑ 이동: 1.0 1.1 1.2 1.3 Markov Chains explained visually
- ↑ 이동: 2.0 2.1 2.2 Markov Chain - an overview
- ↑ 이동: 3.0 3.1 3.2 3.3 Introduction to Markov Chains
- ↑ Brilliant Math & Science Wiki
- ↑ Markov Chain - an overview
- ↑ 이동: 6.0 6.1 6.2 6.3 Markov chain
- ↑ 이동: 7.0 7.1 7.2 7.3 First Links in the Markov Chain
- ↑ 이동: 8.0 8.1 8.2 8.3 Estimating the number and length of episodes in disability using a Markov chain approach
- ↑ 이동: 9.0 9.1 Origin of Markov chains (video)
- ↑ 이동: 10.0 10.1 Definition:
- ↑ 이동: 11.0 11.1 11.2 11.3 A New Multivariate Markov Chain Model for Adding a New Categorical Data Sequence
- ↑ Markov Chain -- from Wolfram MathWorld
- ↑ 이동: 13.0 13.1 13.2 13.3 Mission 2: Markov Chains
- ↑ Stochastically monotone Markov Chains
- ↑ Geyer : Practical Markov Chain Monte Carlo
- ↑ 이동: 16.0 16.1 16.2 16.3 Predictive Bayesian selection of multistep Markov chains, applied to the detection of the hot hand and other statistical dependencies in free throws
- ↑ 이동: 17.0 17.1 17.2 17.3 (Tutorial) Markov Chains in Python
- ↑ 이동: 18.0 18.1 18.2 18.3 Markov Chains: From Theory to Implementation and Experimentation
- ↑ Quantum Markov chains
- ↑ 이동: 20.0 20.1 20.2 20.3 Markov Chain Modeling of Sequences of Lagged NWP Ensemble Probability Forecasts: An Exploration of Model Properties and Decision Support Applications
- ↑ 이동: 21.0 21.1 21.2 21.3 Markov Chains
- ↑ 이동: 22.0 22.1 22.2 22.3 Markov Chain
- ↑ Introduction
- ↑ 이동: 24.0 24.1 24.2 24.3 Markov Chain Monte Carlo in Practice
관련 링크
메타데이터
위키데이터
- ID : Q176645
Spacy 패턴 목록
- [{'LOWER': 'markov'}, {'LEMMA': 'chain'}]
- [{'LOWER': 'markov'}, {'LEMMA': 'process'}]
- [{'LOWER': 'markov'}, {'LEMMA': 'chain'}]