자연상수 e

수학노트
둘러보기로 가기 검색하러 가기

개요

  • 다음 수열의 극한을 통해 정의됨\[e=\lim_{n\to \infty}(1 + \frac{1}{n})^n = 2.7182818284590452353602874713526624977572470936999595749669676277240\cdots\]
    • 이 수열은 느리게 수렴함
  • 급수를 통한 표현\[e=\sum_{n=0}^{\infty}\frac{1}{n!}\]
    • 이 급수는 빠르게 수렴함
  • 미적분학에서 가장 중요한 역할을 하는 수의 하나로 다음 함수들을 정의할 수 있게 해줌
    • 지수함수 \(e^x\)
    • 자연로그함수 \(\ln x = \log_{e} x\)


이자율을 통한 이해

수열에 친숙해지기 위하여 좀더 친숙한 상황을 하나 생각해 보자.

자연상수를 공부하기엔, 돈과 이자 얘기가 좋다. 복리로 주어지는 예금상품이 있다고 하자. 넣어둔 돈이 a이고, 단위기간 동안의 이자율이 r이라고 하면, 그 단위기간이 지났을 때, 돈은 a(1+r) 이 된다. 만약에 그 돈을 계속 넣어둔다면, 약속된 단위기간이 지날 때마다, 통장의 예금 \[a(1+r), a(1+r)^2, a(1+r)^3, \cdots, a(1+r)^n, \cdots\]

로 늘어나게 된다.

이제 자연상수를 공부하기 위하여, 넣어둔 돈은 1, 단위기간은 1년, 이자율은 100%라고 하자.(말하고 보니, 이데아의 세계…) 1년 뒤에는 돈이 2가 될 것이다. 그런데 이 상황을 약간 변형하여 이렇게 하면 어떨까. 단위기간은 1년의 절반인 6개월로 하는 대신, 이자를 6개월마다 50% 복리로 받는 것이다. 그렇다면 1년 후에, 통장에 들어 있게 되는 돈은 다음과 같다. \[(1 + \frac{1}{2})^2 = 2.25\]

수익이 더 높아졌다!

만약에 단위기간을 1년의 3분의 1인, 4개월로 하고, 4개월마다 이자를 33.33% 씩 받는다면, 1년 후에 받게 되는 돈은 이렇게 될 것이다.

\[(1+\frac{1}{3})^3 = 2.3703704\cdots\]

수익이 더 높아졌다. 이자를 이런 식으로 받으면 수익은 언제나 더 높아지는 것일까? 즉, 만약 단위기간을 1년의 n분의 1로 하고, 이자를 n분의 1 비율의 복리로 받게 된다면, 1년후, 이 돈은 얼마가 되는 것일까. 이렇게 될 것이다.

\[(1 + \frac{1}{n})^n\]

이제 오늘 내가 할 것은, 바로 이 수열에 대한 것이다.

  1. 이자율은 아무리 잘게 쪼개도 200%는 안 된다.
  2. 그렇지만 이자를 잘게 쪼개서 받을수록 수익률은 더 높다.

이 두가지 사실이 수학적으로 의미하는 사실은,

ㅣ\((1 + \frac{1}{n})^n\)

이라는 수열은, 유계인 단조증가 수열이라는 것이다. 따라서 지난번 “리만의 제타함수 (5) : 지수의 실수로의 확장“에서 언급한, 실수의 완비성에 의해, 이 수열은 수렴하게 된다. 이 때, 수열의 극한값을 e, 자연상수라고 부르는 것이다.


수열


\((1 + \frac{1}{n})^n<3\) 의 증명

\((1 + \frac{1}{n})^n\)는 증가수열 및 자연상수의 정의.



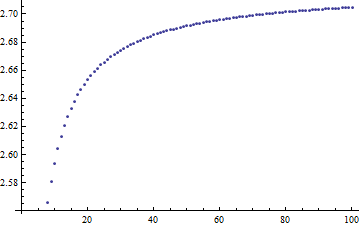
수열의 수렴

  • 정의에 사용된 수열은 매우 느리게 수렴함

\[a_n=(1 + \frac{1}{n})^n\]

3623769-e.gif

  • \(a_1\)부터 \(a_{20}\)까지의 값 2.0000000000000000000 2.2500000000000000000 2.3703703703703703704 2.4414062500000000000 2.4883200000000000000 2.5216263717421124829 2.5464996970407131139 2.5657845139503479004 2.5811747917131971820 2.5937424601000000000 2.6041990118975308782 2.6130352902246781603 2.6206008878857322211 2.6271515563008693884 2.6328787177279190470 2.6379284973665998588 2.6424143751831096203 2.6464258210976854673 2.6500343266404449073 2.6532977051444201339



급수의 수렴

  • 다음 급수는 빠르게 자연상수로 수렴하므로 자연상수의 십진법 전개를 계산하는데 사용될 수 있음\[b_n=\sum_{k=0}^{n}\frac{1}{k!}\]
  • \(b_1\)부터 \(b_{20}\)까지의 값 2.00000000000000000000000000000 2.50000000000000000000000000000 2.66666666666666666666666666667 2.70833333333333333333333333333 2.71666666666666666666666666667 2.71805555555555555555555555556 2.71825396825396825396825396825 2.71827876984126984126984126984 2.71828152557319223985890652557 2.71828180114638447971781305115 2.71828182619849286515953182620 2.71828182828616856394634172412 2.71828182844675900231455787011 2.71828182845822974791228759483 2.71828182845899446428546957647 2.71828182845904225905879345033 2.71828182845904507051604779585 2.71828182845904522670811748171 2.71828182845904523492875272834 2.71828182845904523533978449067


자연상수의 소수점 1000자리까지의 전개

  • 소수점 1000자리 십진전개 2.71828182845904523536028747135266249775724709369995957496696762772407\ 6630353547594571382178525166427427466391932003059921817413596629043572\ 9003342952605956307381323286279434907632338298807531952510190115738341\ 8793070215408914993488416750924476146066808226480016847741185374234544\ 2437107539077744992069551702761838606261331384583000752044933826560297\ 6067371132007093287091274437470472306969772093101416928368190255151086\ 5746377211125238978442505695369677078544996996794686445490598793163688\ 9230098793127736178215424999229576351482208269895193668033182528869398\ 4964651058209392398294887933203625094431173012381970684161403970198376\ 7932068328237646480429531180232878250981945581530175671736133206981125\ 0996181881593041690351598888519345807273866738589422879228499892086805\ 8257492796104841984443634632449684875602336248270419786232090021609902\ 3530436994184914631409343173814364054625315209618369088870701676839642\ 4378140592714563549061303107208510383750510115747704171898610687396965\ 521267154688957035035




재미있는 사실

  • \(e^{-e}<x<e^{1/e}\) 인 x에 대해 \({{{x^x}^x}^x}^{...}\)은 극한을 갖는다.



역사



메모

관련된 항목들



사전 형태의 자료



관련논문과 에세이


관련도서

  • 오일러가 사랑한 수 e (경문수학산책16) e : (The) Story of a number
    • 엘리 마오 지음, 허민, 옮김, 경문사, 2000-12-01



관련기사


블로그

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LEMMA': 'e'}]
  • [{'LOWER': 'euler'}, {'LOWER': "'s"}, {'LEMMA': 'number'}]
  • [{'LOWER': 'napier'}, {'LOWER': "'s"}, {'LEMMA': 'constant'}]
  • [{'LOWER': 'natural'}, {'LEMMA': 'constant'}]
  • [{'LEMMA': '2.71828'}]
  • [{'LEMMA': '2.718281828'}]
  • [{'OP': '*'}, {'LOWER': '1'}, {'LOWER': '+'}, {'LOWER': '1'}, {'LOWER': '/'}, {'LEMMA': 'n)^n'}]
  • [{'LEMMA': '𝑒'}]
  • [{'LEMMA': 'ε'}]
  • [{'LOWER': 'e'}, {'OP': '*'}, {'LOWER': 'mathematical'}, {'LOWER': 'constant'}, {'LEMMA': ')'}]
  • [{'LEMMA': '2.718'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=자연상수_e&oldid=52446"