체커보드의 원근법
둘러보기로 가기
검색하러 가기
개요
- 체커보드 또는 pavimenti 그리기
- 원근법이 사용된 그림에서 바닥의 정사각형 타일을 많이 볼 수 있다 (예를 들면, 베르미어의 여러 작품들)
- 그리기를 진행하다보면 여러 개의 점이 한 직선 위에 놓여있는 것(공선성, collinearity)과 같은 자명하지 않은 수학적 현상을 만나게 된다
- 여러 점들의 공선성은 데자르그의 정리 등 사영기하학의 주요 결과를 이용하여 보일 수 있음
체커보드
위의 장면을 특정한 위치에서 바라보며 그림으로 옮긴다면, 다음과 같이 될 것이다.
그림을 그리는 절차와 수학적 질문
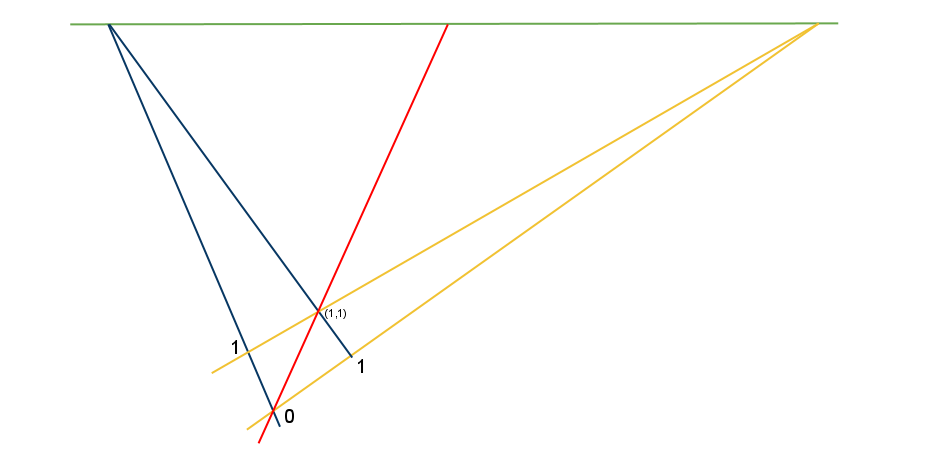
그림을 그리는 절차에 대해서 생각해 보자. 다음과 같은 그림에서 시작하자. 이는 두 평행선이 지평선에서 만나도록 하여 하나의 정사각형을 그린 것이다.
격자를 그림으로 옮기기 위해 기존의 그림에 새로운 직선을 추가하는 원칙은 단순하다 :
- 정사각형으로 구성된 체커보드에서 여러 직선들이 서로 만나는 점은 그림 속에서도 그 직선들이 만나는 점으로 그려져야 한다. (이는 당연한 원칙이다. 수학적으로 말하자면 incidence 관계의 보존)
- 모든 평행선은 지평선 (초록색 선)에서 만난다. (이것은 그다지 당연하지 않은 원근법의 핵심에 있는 원칙이다)
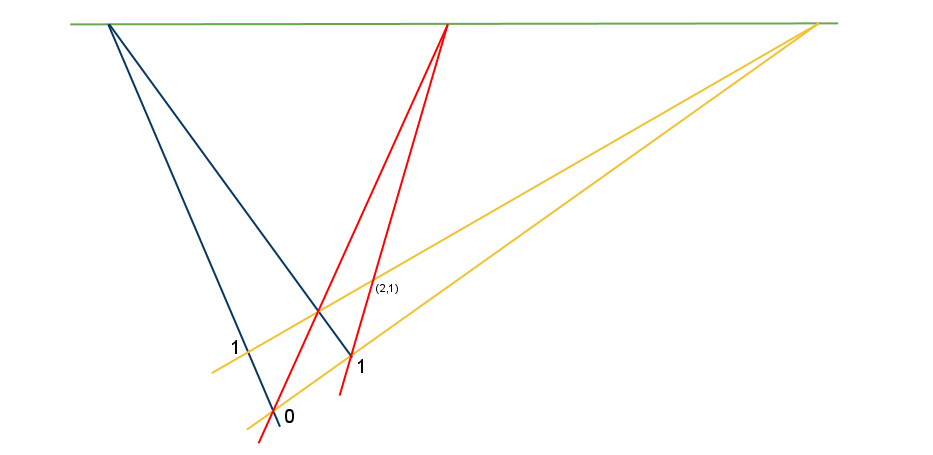
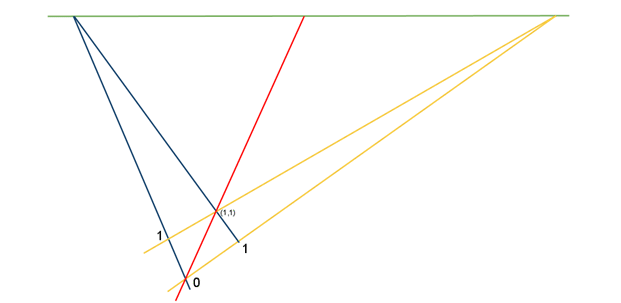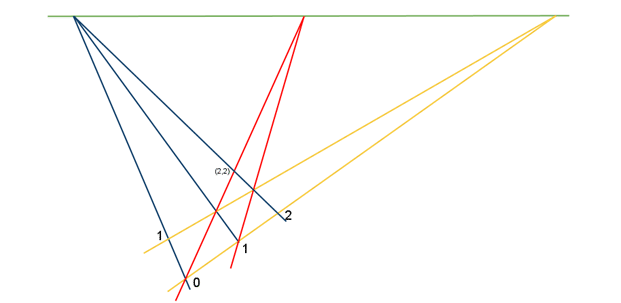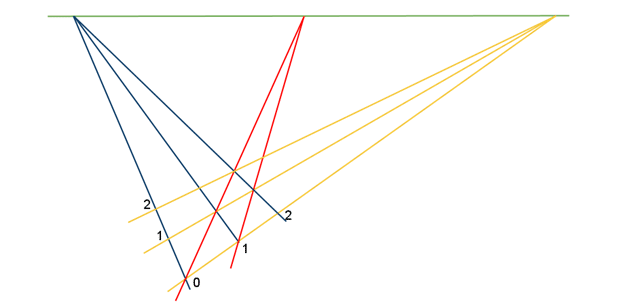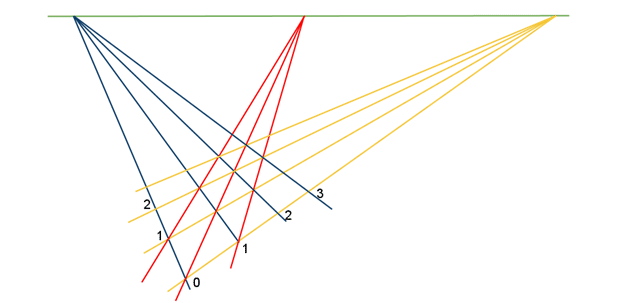
위의 그림에 새로운 빨간색 선을 아래와 같이 추가한다.
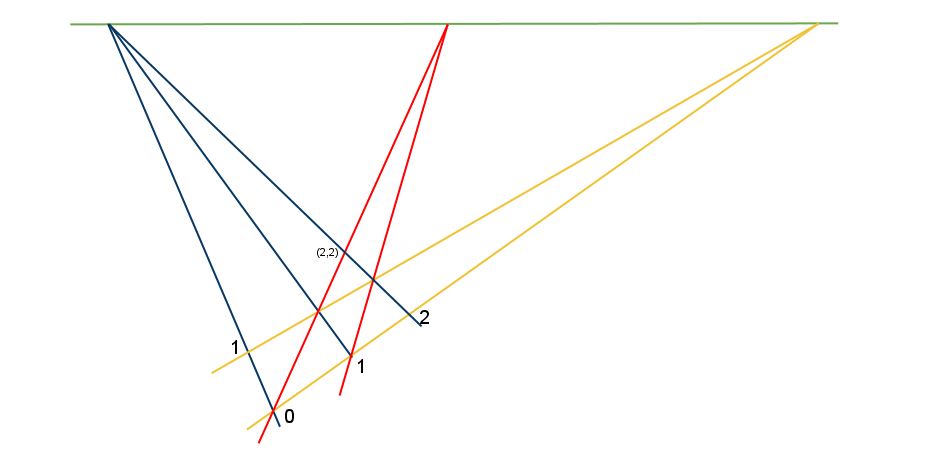
파란색 선을 다음과 같이 추가한다.
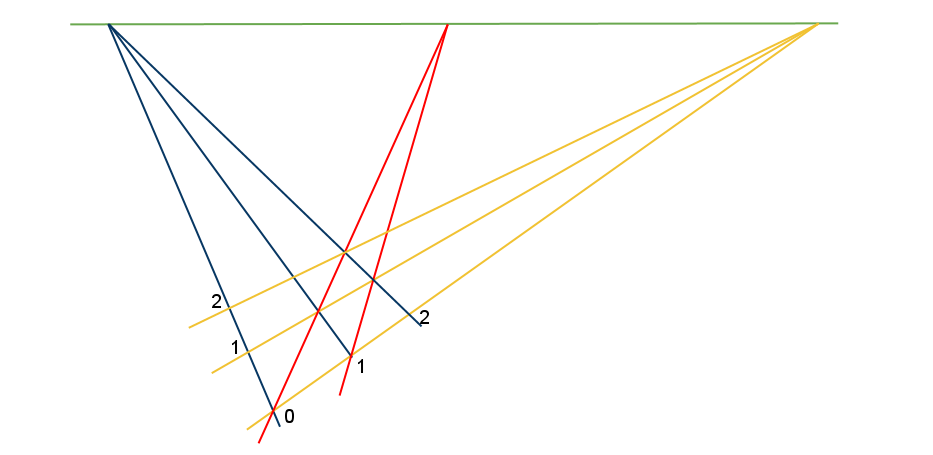
노란색 선을 다음과 같이 추가한다.
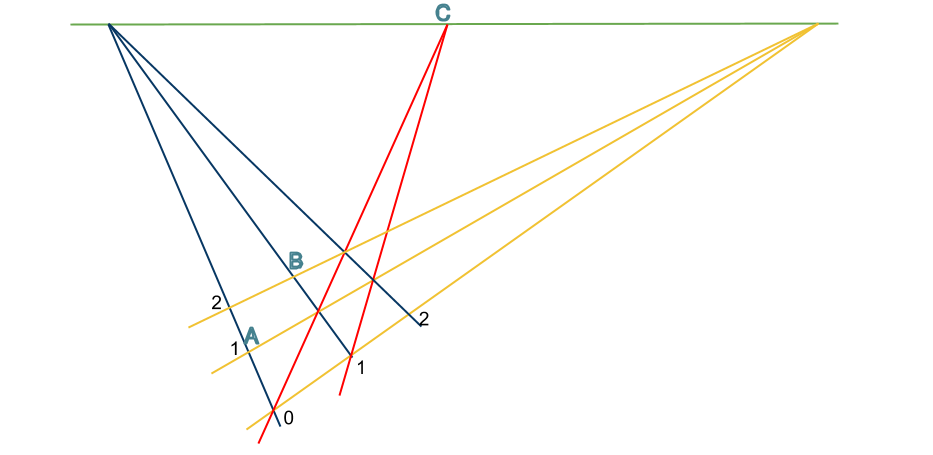
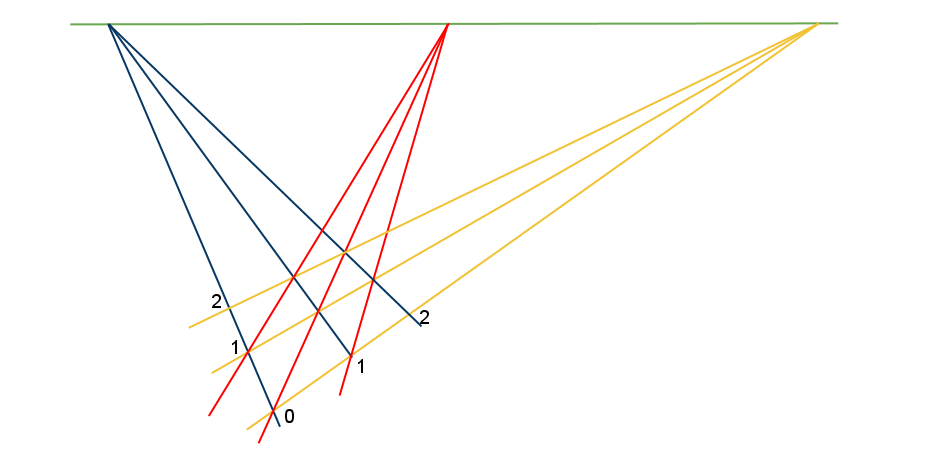
이제 아래의 그림에 빨간색 선을 하나 더 추가하려는 순간, 우리는 다음과 같은 자명하지 않은 수학적 질문을 마주하게 된다.
세 점 A,B,C는 한 직선 위에 놓여 있는가?
이는 원근법이 일관성있는 그리기의 법칙이 되기 위해서는 수학적 원리에 의해 정당화될 필요가 있다는 것을 의미한다.
동영상
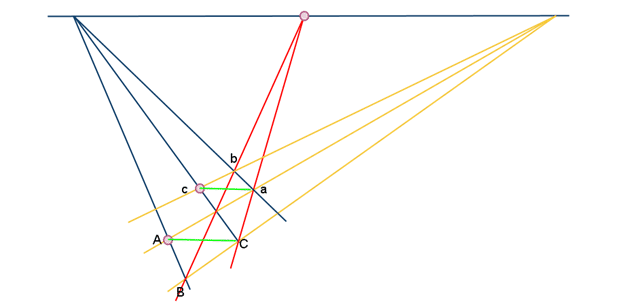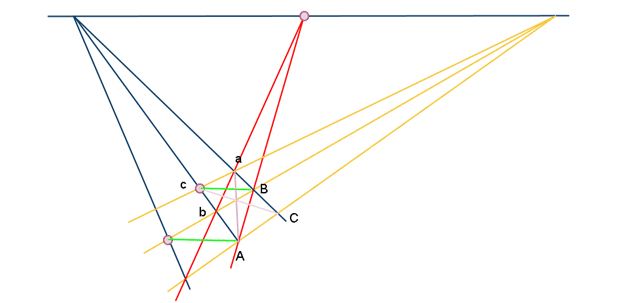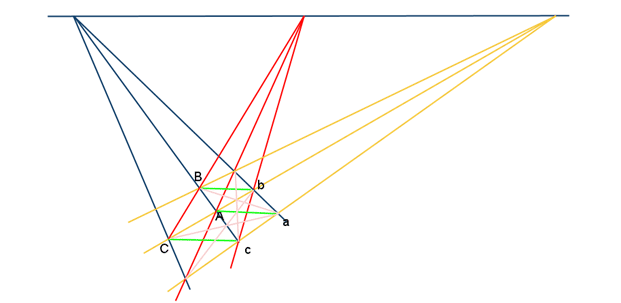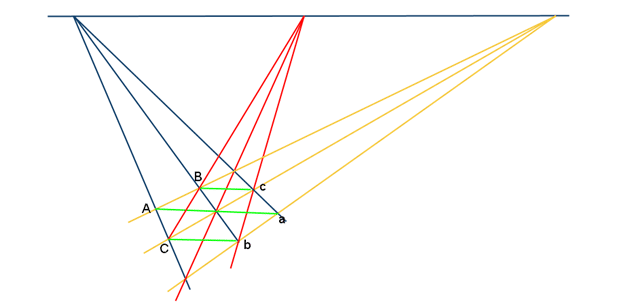
공선성(collinearity)의 증명
- 데자르그의 정리를 반복 적용하여 보일 수 있다
- 아래 그림에서 나타나는 두 삼각형 ABC와 abc 는 중심배경(central perspectivity) 또는 축배경(axial perspectivity) 에 놓여있다
메모
- Alberti's Construction
- Distance Point Construction
- Equivalence of Alberti's and the Distance Point Construction
- costruzione legittima
- http://www.wegehenkel.com/artwork_drawingcrs_perspective.html
- http://www.youtube.com/watch?v=pkEPXJU-36s
관련된 항목들
에세이, 강의노트
- Kandra Wynne Bellanca, Perspective on Pavimenti :finding perspective mathematically, 2007
관련도서
- Stillwell, John. Yearning for the Impossible: The Surprising Truths of Mathematics. Peters, 2006.
수학용어번역
- collinear - 대한수학회 수학용어집
- 동일직선상(의), 공선
- 단어사전