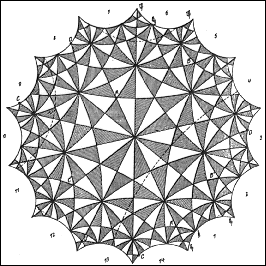
"클라인의 4차곡선"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
(피타고라스님이 이 페이지의 클라인의_4차곡선.nb 파일을 삭제하였습니다.) |
Pythagoras0 (토론 | 기여) |
||
| (사용자 2명의 중간 판 18개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | + | ==개요== | |
| − | + | * 종수(genus)가 3인 복소대수곡선 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * 종수(genus)가 3인 복소대수곡선 | ||
** <math>\mathbb CP^2</math> 에서 <math>x^3y+y^3z+z^3x=0</math> 로 주어진 (복소) 대수곡선 | ** <math>\mathbb CP^2</math> 에서 <math>x^3y+y^3z+z^3x=0</math> 로 주어진 (복소) 대수곡선 | ||
| − | ** [[푸앵카레 상반평면 모델|푸앵카레 상반평면]] | + | ** [[푸앵카레 상반평면 모델|푸앵카레 상반평면]]을 universal covering으로 갖는 쌍곡기하학의 곡면:<math>\mathbb H^2/\Gamma(7)</math>:<math>\Gamma(7)=\left\{\begin{bmatrix} a&b \\ c&d \end{bmatrix} \in SL(2,\mathbb Z) : \begin{bmatrix} a&b \\ c&d \end{bmatrix} \equiv \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} \pmod 7\right\}</math> |
| − | * [[쌍곡기하학]] 세계의 Platonic solid, | + | * [[쌍곡기하학]] 세계의 플라톤 다면체(Platonic solid), 즉 [[정다면체]] |
** 정칠각형으로 24조각으로 만들어진 정이십사면체 | ** 정칠각형으로 24조각으로 만들어진 정이십사면체 | ||
| − | ** 자기동형군, 즉 대칭군은 PSL(2,7)와 동형임. | + | ** 자기동형군, 즉 대칭군은 <math>\operatorname{PSL}(2,\mathbb{F}_ 7)</math>와 동형임. |
** 168가지의 대칭을 가짐 | ** 168가지의 대칭을 가짐 | ||
| − | + | ||
| + | ==주기 행렬== | ||
| + | * [[클라인 4차곡선의 주기 행렬]] | ||
| + | :<math> | ||
| + | \frac{1}{2} \left( | ||
| + | \begin{array}{ccc} | ||
| + | \rho & 1 & 1 \\ | ||
| + | 1 & \rho & 1 \\ | ||
| + | 1 & 1 & \rho \\ | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | 여기서 <math>\rho=\frac{-1+\sqrt{-7}}{2}</math>. | ||
| − | |||
| − | + | ==자기동형군== | |
* <math>x^3y+y^3z+z^3x=0</math> | * <math>x^3y+y^3z+z^3x=0</math> | ||
| − | * order 3 | + | * order 3 x-> y-> z-> x |
| − | * order 7 | + | * order 7 x->ax, y->by, z->cz for some a,b,c we want <math>a^3b=b^3c=c^3a</math> solution : <math> a=\zeta^4, b=\zeta^2,c=\zeta^1</math> where <math>\zeta^7=1</math> |
| − | + | ||
| − | + | ==PSL(2,7)== | |
* PSL(2,7) (isomorphic PSL(3,2)) has order 168 | * PSL(2,7) (isomorphic PSL(3,2)) has order 168 | ||
| − | * GL(2,7) has order (7^2-1)(7^2-7) | + | * GL(2,7) has order <math>(7^2-1)(7^2-7)</math> |
| − | * SL(2,7) has order (7^2-1)7=6\times 7\times 8 | + | * SL(2,7) has order <math>(7^2-1)7=6\times 7\times 8</math> |
| − | * PSL(2,7) has order 6\times 7\times 8/2 | + | * PSL(2,7) has order <math>6\times 7\times 8/2</math> |
| − | * 크기가 가장 작은 후르비츠 군이다 | + | * 크기가 가장 작은 후르비츠 군이다 <math>a^2=b^3=c^7=abc=1</math>. 여기서 <math>a=S, b=ST, c=T</math> 로 두면 된다 (S,T는 [[모듈라 군(modular group)]] 의 원소) |
| − | + | :<math>S=\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix},T=\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} </math> | |
| − | + | * PSL(2,7)은 3차원 표현을 가지므로 <math> \mathbb{C}[x,y,z]</math>에 작용한다. | |
| − | + | * any polynomial invariant under PSL(2,7) also invariant under subgroup of order 21. | |
| − | + | * (generated by order 3 transformation <math>x\to y\to z\to x</math> and order 7 transformation <math>x\to ax, y\to by, z\to cz</math> where <math>a=\zeta^4, b=\zeta^2,c=\zeta^1</math> where <math>\zeta^7=1</math>) | |
| − | + | * Not many invariant elements of degree 4. | |
| − | PSL(2,7)은 3차원 표현을 가지므로 \mathbb{C}[x,y,z]에 작용한다. | + | * Only monomials of degree 4 invariant under elements of order 7 are <math>x^3y,y^3z,z^3x</math>. |
| − | + | * If in addition we require invariance under <math>x\to y\to z\to x</math>, only possibility is <math>\text{constant} \times (x^3y+y^3z+z^3x)</math>. | |
| − | any polynomial invariant under PSL(2,7) also invariant under subgroup of order 21. | + | * If any Hurwitz group acts on a curve, then PSL(2,7) acts on <math>x^3y+y^3z+z^3x=0</math> |
| − | |||
| − | (generated by order 3 transformation x | ||
| − | |||
| − | Not many invariant elements of degree 4. | ||
| − | |||
| − | Only monomials of degree 4 invariant under elements of order 7 are x^3y,y^3z,z^3x. | ||
| − | |||
| − | If in addition we require invariance under x | ||
| − | |||
| − | If any Hurwitz group acts on a curve, then PSL(2,7) acts on x^3y+y^3z+z^3x=0 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ==(2,3,7) 삼각형== | |
| − | * 삼각형의 세 각이 각각 | + | * 삼각형의 세 각이 각각:<math>\frac{\pi}{7},\frac{\pi}{3},\frac{\pi}{2}</math> 로 주어지며, 이 세각의 크기를 모두 더하면,:<math>\frac{\pi}{7}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{41\pi}{42}</math> 가 되어, 180도보다 작게 된다. |
* '''쌍곡기하학에서의 곡률은 음수이기 때문에 나타나는 현상이다.''' | * '''쌍곡기하학에서의 곡률은 음수이기 때문에 나타나는 현상이다.''' | ||
* [[쌍곡기하학]] 항목 참조 | * [[쌍곡기하학]] 항목 참조 | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ==전개도== | |
| − | + | ||
| − | + | [[파일:3063024-klein.gif]] | |
| − | + | ||
| − | + | ||
| − | |||
| − | + | ==세타함수== | |
| − | + | * 세타함수:<math>\theta_{7,1}=\sum_{k\in Z}(-1)^{k}q^{\frac{(14k+1)^2}{56}}=q^{1/56}(q^3;q^7)_\infty (q^4; q^7)_\infty(q^7;q^7)_\infty</math>:<math>\theta_{7,3}=\sum_{k\in Z}(-1)^{k}q^{\frac{(14k+3)^2}{56}}=q^{9/56}(q^2;q^7)_\infty (q^5; q^7)_\infty(q^7;q^7)_\infty</math>:<math>\theta_{7,5}=\sum_{k\in Z}(-1)^{k}q^{\frac{(14k+5)^2}{56}}=q^{25/56}(q;q^7)_\infty (q^6; q^7)_\infty(q^7;q^7)_\infty</math> | |
| + | * 세타함수는 클라인 곡선을 매개화한다:<math>x=\theta_{7,1},y=-\theta_{7,5},z=\theta_{7,3}</math> | ||
| + | :<math>x^3y+y^3z+z^3x=0</math> | ||
| + | :<math>xyz=-\eta(\tau)\eta(7\tau)^2</math> | ||
| − | + | ||
| − | + | ||
| − | + | ==조각== | |
| − | + | [[파일:3063024-DSCN4142.JPG|400px]] | |
| − | < | + | ==메모== |
| − | + | * Yang, Lei. 2014. “Dedekind <math>\eta</math>-Function, Hauptmodul and Invariant Theory.” arXiv:1407.3550 [math], July. http://arxiv.org/abs/1407.3550. | |
| − | * A5 다음으로 크기가 작은 비가환 유한단순군이다. 168은 | + | * http://www.youtube.com/watch?v=-FB045lx05M |
| − | * 쌍곡기하학의 정다면체로 이해할 수 있음. | + | * Helaman and Claire Ferguson, [http://www.ams.org/notices/201007/rtx100700840p.pdf Celebrating Mathematics in Stone and Bronze] |
| + | * A5 다음으로 크기가 작은 비가환 유한단순군이다. 168은 7*24, 일주일에 담긴 시간의 수 | ||
| + | * 쌍곡기하학의 정다면체로 이해할 수 있음. | ||
** 정칠각형 24조각 | ** 정칠각형 24조각 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* [http://maxwelldemon.com/2011/10/02/magnetic-klein-quartic/ Magnetic Klein Quartic] | * [http://maxwelldemon.com/2011/10/02/magnetic-klein-quartic/ Magnetic Klein Quartic] | ||
* [http://www.math.uic.edu/%7Eagol/conglink.pdf http://www.math.uic.edu/~agol/conglink.pdf] | * [http://www.math.uic.edu/%7Eagol/conglink.pdf http://www.math.uic.edu/~agol/conglink.pdf] | ||
| − | |||
| − | |||
| − | + | ==매스매티카 파일 및 계산 리소스== | |
* https://docs.google.com/leaf?id=0B8XXo8Tve1cxYjA0YzMzNTYtYzc2Ny00NGE2LWIzY2QtMWU1MTJiODYwM2Y3&sort=name&layout=list&num=50 | * https://docs.google.com/leaf?id=0B8XXo8Tve1cxYjA0YzMzNTYtYzc2Ny00NGE2LWIzY2QtMWU1MTJiODYwM2Y3&sort=name&layout=list&num=50 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==관련된 항목들== | |
* [[컴팩트 리만곡면의 자기동형군에 대한 Hurwitz 정리]] | * [[컴팩트 리만곡면의 자기동형군에 대한 Hurwitz 정리]] | ||
| − | * [[ | + | * [[2차원 쌍곡기하학의 테셀레이션]] |
| − | * [[ | + | * [[반전 사상(inversion)]] |
| − | + | ||
| − | |||
| − | + | ==사전형태의 자료== | |
| + | * http://en.wikipedia.org/wiki/Klein_quartic | ||
| − | + | ||
| − | + | ==관련도서== | |
| − | + | * Edited by Silvio Levy, [http://www.msri.org/publications/books/Book35/contents.html The Eightfold Way: The Beauty of Klein's Quartic Curve] | |
| − | + | ||
| − | |||
| − | + | ||
| − | + | ==관련논문== | |
| − | + | * Martin Deraux, Non-arithmetic lattices and the Klein quartic, arXiv:1605.03846 [math.AG], May 12 2016, http://arxiv.org/abs/1605.03846 | |
| − | + | * Koike, Kenji. ‘The Fermat Septic and the Klein Quartic as Moduli Spaces of Hypergeometric Jacobians’. arXiv:1505.02471 [math], 10 May 2015. http://arxiv.org/abs/1505.02471. | |
| − | + | * [http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mmj&paperid=224&option_lang=eng Ramanujan modular forms and the Klein quartic] | |
| − | * [http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mmj&paperid=224&option_lang=eng Ramanujan modular forms and the Klein quartic] | + | ** G. Lachaud, Mosc. Math. J., 5:4 (2005), 829-856 |
| − | ** G. Lachaud, | + | * King, R. Bruce. ‘Riemann Surfaces as Descriptors for Symmetrical Negative Curvature Carbon and Boron Nitride Structures’. Croatica Chemica Acta 75, no. 2 (3 June 2002): 447–73. |
| − | * [http://arxiv.org/abs/math.NT/0005160 Shimura curve computations] | + | * [http://arxiv.org/abs/math.NT/0005160 Shimura curve computations] |
| − | ** Noam Elkies, | + | ** Noam Elkies, "Algorithmic Number Theory: 3rd International Symposium, ANTS-III; Portland, OR, 6/98: Proceedings", J.P.Buhler, ed.; Lecture Notes in Computer Science, Vol .1423, pages 1-47, 2000 |
| − | + | * [http://www.msri.org/publications/books/Book35/files/klein.pdf On the Order-Seven Transformation of Elliptic Functions] | |
| − | * [http://www.msri.org/publications/books/Book35/files/klein.pdf On the Order-Seven Transformation of Elliptic Functions] | ||
** '''Felix Klein''' (translated by Silvio Levy) | ** '''Felix Klein''' (translated by Silvio Levy) | ||
| − | * [http://www.jstor.org/stable/2974640 A Hyperbolic Plane Coloring and the Simple Group of Order 168] | + | * [http://www.jstor.org/stable/2974640 A Hyperbolic Plane Coloring and the Simple Group of Order 168] |
| − | ** Dana Mackenzie, | + | ** Dana Mackenzie, The American Mathematical Monthly, Vol. 102, No. 8 (Oct., 1995), pp. 706-715 |
| − | * | + | * Prapavessi, Despina T. 1994. “On the Jacobian of the Klein Curve.” Proceedings of the American Mathematical Society 122 (4): 971–978. doi:http://dx.doi.org/10.2307/2161162. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==블로그== | |
| − | + | * [http://bomber0.byus.net/index.php/2007/11/09/467 유한단순군 시간을 말하다], 피타고라스의 창 | |
| + | [[분류:리만곡면론]] | ||
| − | * [ | + | ==메타데이터== |
| − | + | ===위키데이터=== | |
| − | * | + | * ID : [https://www.wikidata.org/wiki/Q977499 Q977499] |
| − | + | ===Spacy 패턴 목록=== | |
| + | * [{'LOWER': 'klein'}, {'LEMMA': 'quartic'}] | ||
2021년 2월 17일 (수) 06:03 기준 최신판
개요
- 종수(genus)가 3인 복소대수곡선
- \(\mathbb CP^2\) 에서 \(x^3y+y^3z+z^3x=0\) 로 주어진 (복소) 대수곡선
- 푸앵카레 상반평면을 universal covering으로 갖는 쌍곡기하학의 곡면\[\mathbb H^2/\Gamma(7)\]\[\Gamma(7)=\left\{\begin{bmatrix} a&b \\ c&d \end{bmatrix} \in SL(2,\mathbb Z) : \begin{bmatrix} a&b \\ c&d \end{bmatrix} \equiv \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} \pmod 7\right\}\]
- 쌍곡기하학 세계의 플라톤 다면체(Platonic solid), 즉 정다면체
- 정칠각형으로 24조각으로 만들어진 정이십사면체
- 자기동형군, 즉 대칭군은 \(\operatorname{PSL}(2,\mathbb{F}_ 7)\)와 동형임.
- 168가지의 대칭을 가짐
주기 행렬
\[ \frac{1}{2} \left( \begin{array}{ccc} \rho & 1 & 1 \\ 1 & \rho & 1 \\ 1 & 1 & \rho \\ \end{array} \right) \] 여기서 \(\rho=\frac{-1+\sqrt{-7}}{2}\).
자기동형군
- \(x^3y+y^3z+z^3x=0\)
- order 3 x-> y-> z-> x
- order 7 x->ax, y->by, z->cz for some a,b,c we want \(a^3b=b^3c=c^3a\) solution \[ a=\zeta^4, b=\zeta^2,c=\zeta^1\] where \(\zeta^7=1\)
PSL(2,7)
- PSL(2,7) (isomorphic PSL(3,2)) has order 168
- GL(2,7) has order \((7^2-1)(7^2-7)\)
- SL(2,7) has order \((7^2-1)7=6\times 7\times 8\)
- PSL(2,7) has order \(6\times 7\times 8/2\)
- 크기가 가장 작은 후르비츠 군이다 \(a^2=b^3=c^7=abc=1\). 여기서 \(a=S, b=ST, c=T\) 로 두면 된다 (S,T는 모듈라 군(modular group) 의 원소)
\[S=\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix},T=\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \]
- PSL(2,7)은 3차원 표현을 가지므로 \( \mathbb{C}[x,y,z]\)에 작용한다.
- any polynomial invariant under PSL(2,7) also invariant under subgroup of order 21.
- (generated by order 3 transformation \(x\to y\to z\to x\) and order 7 transformation \(x\to ax, y\to by, z\to cz\) where \(a=\zeta^4, b=\zeta^2,c=\zeta^1\) where \(\zeta^7=1\))
- Not many invariant elements of degree 4.
- Only monomials of degree 4 invariant under elements of order 7 are \(x^3y,y^3z,z^3x\).
- If in addition we require invariance under \(x\to y\to z\to x\), only possibility is \(\text{constant} \times (x^3y+y^3z+z^3x)\).
- If any Hurwitz group acts on a curve, then PSL(2,7) acts on \(x^3y+y^3z+z^3x=0\)
(2,3,7) 삼각형
- 삼각형의 세 각이 각각\[\frac{\pi}{7},\frac{\pi}{3},\frac{\pi}{2}\] 로 주어지며, 이 세각의 크기를 모두 더하면,\[\frac{\pi}{7}+\frac{\pi}{3}+\frac{\pi}{2}=\frac{41\pi}{42}\] 가 되어, 180도보다 작게 된다.
- 쌍곡기하학에서의 곡률은 음수이기 때문에 나타나는 현상이다.
- 쌍곡기하학 항목 참조
전개도
세타함수
- 세타함수\[\theta_{7,1}=\sum_{k\in Z}(-1)^{k}q^{\frac{(14k+1)^2}{56}}=q^{1/56}(q^3;q^7)_\infty (q^4; q^7)_\infty(q^7;q^7)_\infty\]\[\theta_{7,3}=\sum_{k\in Z}(-1)^{k}q^{\frac{(14k+3)^2}{56}}=q^{9/56}(q^2;q^7)_\infty (q^5; q^7)_\infty(q^7;q^7)_\infty\]\[\theta_{7,5}=\sum_{k\in Z}(-1)^{k}q^{\frac{(14k+5)^2}{56}}=q^{25/56}(q;q^7)_\infty (q^6; q^7)_\infty(q^7;q^7)_\infty\]
- 세타함수는 클라인 곡선을 매개화한다\[x=\theta_{7,1},y=-\theta_{7,5},z=\theta_{7,3}\]
\[x^3y+y^3z+z^3x=0\] \[xyz=-\eta(\tau)\eta(7\tau)^2\]
조각
메모
- Yang, Lei. 2014. “Dedekind \(\eta\)-Function, Hauptmodul and Invariant Theory.” arXiv:1407.3550 [math], July. http://arxiv.org/abs/1407.3550.
- http://www.youtube.com/watch?v=-FB045lx05M
- Helaman and Claire Ferguson, Celebrating Mathematics in Stone and Bronze
- A5 다음으로 크기가 작은 비가환 유한단순군이다. 168은 7*24, 일주일에 담긴 시간의 수
- 쌍곡기하학의 정다면체로 이해할 수 있음.
- 정칠각형 24조각
- Magnetic Klein Quartic
- http://www.math.uic.edu/~agol/conglink.pdf
매스매티카 파일 및 계산 리소스
관련된 항목들
사전형태의 자료
관련도서
- Edited by Silvio Levy, The Eightfold Way: The Beauty of Klein's Quartic Curve
관련논문
- Martin Deraux, Non-arithmetic lattices and the Klein quartic, arXiv:1605.03846 [math.AG], May 12 2016, http://arxiv.org/abs/1605.03846
- Koike, Kenji. ‘The Fermat Septic and the Klein Quartic as Moduli Spaces of Hypergeometric Jacobians’. arXiv:1505.02471 [math], 10 May 2015. http://arxiv.org/abs/1505.02471.
- Ramanujan modular forms and the Klein quartic
- G. Lachaud, Mosc. Math. J., 5:4 (2005), 829-856
- King, R. Bruce. ‘Riemann Surfaces as Descriptors for Symmetrical Negative Curvature Carbon and Boron Nitride Structures’. Croatica Chemica Acta 75, no. 2 (3 June 2002): 447–73.
- Shimura curve computations
- Noam Elkies, "Algorithmic Number Theory: 3rd International Symposium, ANTS-III; Portland, OR, 6/98: Proceedings", J.P.Buhler, ed.; Lecture Notes in Computer Science, Vol .1423, pages 1-47, 2000
- On the Order-Seven Transformation of Elliptic Functions
- Felix Klein (translated by Silvio Levy)
- A Hyperbolic Plane Coloring and the Simple Group of Order 168
- Dana Mackenzie, The American Mathematical Monthly, Vol. 102, No. 8 (Oct., 1995), pp. 706-715
- Prapavessi, Despina T. 1994. “On the Jacobian of the Klein Curve.” Proceedings of the American Mathematical Society 122 (4): 971–978. doi:http://dx.doi.org/10.2307/2161162.
블로그
- 유한단순군 시간을 말하다, 피타고라스의 창
메타데이터
위키데이터
- ID : Q977499
Spacy 패턴 목록
- [{'LOWER': 'klein'}, {'LEMMA': 'quartic'}]