푸앵카레 상반평면 모델

수학노트
둘러보기로 가기 검색하러 가기

개요



정의

  • \(\mathbb{H}^2=\{z=x+iy\in\mathbb{C}|y>0\}\)



제1기본형식

  • 리만 메트릭\[ds^2=\frac{dx^2+dy^2}{y^2}=\frac{dzd\overline{z}}{y^2}\]
  • \(E=1/y^2\)
  • \(F=0\)
  • \(G=1/y^2\)
  • 면적소\[dA=\frac{dx\,dy}{y^2}\]
  • 두 점 사이의 거리

\[\rho(z_ 1,z_ 2)=2\tanh^{-1}\frac{|z_ 1-z_ 2|}{|z_ 1-\overline{z_ 2}|}\] \[ \cosh \rho(z_ 1,z_ 2)=1+\frac{|z_1-z_2|^2}{2y_1y_2}= \frac{\left(x_1-x_2\right)^2+y_1^2+y_2^2}{2 y_1 y_2} \]



크리스토펠 기호

  • 크리스토펠 기호\[\begin{array}{ll} \Gamma _ {11}^1 & 0 \\ \Gamma _ {12}^1 & -\frac{1}{y} \\ \Gamma _ {21}^1 & -\frac{1}{y} \\ \Gamma _ {22}^1 & 0 \\ \Gamma _ {11}^2 & \frac{1}{y} \\ \Gamma _ {12}^2 & 0 \\ \Gamma _ {21}^2 & 0 \\ \Gamma _ {22}^2 & -\frac{1}{y} \end{array}\]
  • 등장변환군(isometry group)

\[\operatorname{PSL}(2,\mathbb{R})\rtimes \mathbb{Z}/2\mathbb{Z}\]


라플라시안

  • 라플라시안\[\Delta f=y^2(\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2})\]



측지선

  • 측지선이 만족시키는 미분방정식은 다음과 같다

\[\left\{ \begin{array}{c} \frac{d^2 x }{dt^2} + \Gamma^{1}_{1 2 }\frac{dx }{dt}\frac{dy }{dt} +\Gamma^{1}_{2 1 }\frac{dx }{dt}\frac{dy }{dt}= 0 \\ \frac{d^2 y }{dt^2} + \Gamma^{2}_{1 1 }\frac{dx }{dt}\frac{dx }{dt} +\Gamma^{2}_{2 2 }\frac{dy }{dt}\frac{dy }{dt} = 0 \end{array} \right. \]

  • 다시 쓰면 다음과 같다

\[ \left\{ \begin{array}{c} \ddot{x}y-2\dot{x}\dot{y}=0 \\ \ddot{y}y+(\dot{x})^2-(\dot{y})^2=0 \end{array} \right. \]

  • 미분방정식의 해는 적당한 상수 a,b,c,r 에 대하여 다음과 같이 주어진다
    • \((x(t),y(t))\)로 매개화된 실직선에 수직인 반원 \[\left\{ \begin{array}{c} x(t)=a+b\tanh(rt+c) \\ y(t)=b\operatorname{sech}(rt+c) \end{array} \right. \] \(\tanh ^{2}x=1-\operatorname{sech}^{2}x\) 쌍곡함수)
    • \((x(t),y(t))\)로 매개화된 y-축과 평행한 직선 \[\left\{ \begin{array}{c} x(t)=a \\ y(t)=be^{rt+c} \end{array} \right. \]
  • http://cktalon.wordpress.com/2010/10/22/geodesics-poincare-half-plane/


리만 텐서

\(\begin{array}{ll} \begin{array}{ll} R_ {111}^1 & 0 \\ R_ {112}^1 & 0 \end{array} & \begin{array}{ll} R_ {121}^1 & 0 \\ R_ {122}^1 & 0 \end{array} \\ \begin{array}{ll} R_ {211}^1 & 0 \\ R_ {212}^1 & -\frac{1}{y^2} \end{array} & \begin{array}{ll} R_ {221}^1 & \frac{1}{y^2} \\ R_ {222}^1 & 0 \end{array} \\ \begin{array}{ll} R_ {111}^2 & 0 \\ R_ {112}^2 & \frac{1}{y^2} \end{array} & \begin{array}{ll} R_ {121}^2 & -\frac{1}{y^2} \\ R_ {122}^2 & 0 \end{array} \\ \begin{array}{ll} R_ {211}^2 & 0 \\ R_ {212}^2 & 0 \end{array} & \begin{array}{ll} R_ {221}^2 & 0 \\ R_ {222}^2 & 0 \end{array} \end{array}\)



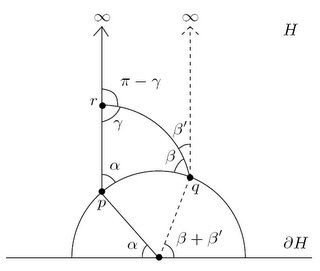
쌍곡삼각형의 넓이

Hyperbolic triangle.jpg

  • 삼각형\(D=pq\infty\)의 넓이\[x(P)\] 를 점 \(P\)의 \(x\)좌표라 하고, \(x(p)=a\), \(x(q)=b\)라 두자. \[A(D)=\int\int_{D}\frac{dx\,dy}{y^2}=\int_{a}^{b}\int_{\sqrt{1-x^2}}^{\infty}\frac{dy\,dx}{y^2}=\int_{a}^{b}\frac{1}{\sqrt{1-x^2}}\,dx=-\int_{\pi-\alpha}^{\beta+\beta'}\,d\theta=\pi-\alpha-\beta-\beta'\]\[x=\cos \theta\]로 치환, \(a=\cos (\pi-\alpha)\), \(b=\cos (\beta+\beta')\)을 사용하였음
  • 삼각형 \(D'=rq\infty\)의 넓이 위에서 얻은 결과를 적용할 수 있다 \[A(D')=\pi-(\pi-\gamma)-\beta'=\gamma-\beta'\]


(정리)

세 각이 \(\alpha, \beta, \gamma\)인 쌍곡삼각형 \(\Delta\)의 넓이는 \(\pi - \alpha- \beta- \gamma\) 로 주어진다.


(증명)

\(A(\Delta)=A(D)-A(D')=\pi-\alpha-\beta-\beta'-(\gamma-\beta')=\pi - \alpha- \beta- \gamma\) ■




역사



메모



관련된 항목들



매스매티카 파일 및 계산 리소스


수학용어번역

  • isometry - 대한수학회 수학용어집


사전 형태의 자료

메타데이터

메타데이터

위키데이터

Spacy 패턴 목록

  • [{'LOWER': 'poincaré'}, {'LOWER': 'half'}, {'OP': '*'}, {'LOWER': 'plane'}, {'LEMMA': 'model'}]
  • [{'LOWER': 'poincare'}, {'LOWER': 'half'}, {'OP': '*'}, {'LOWER': 'plane'}, {'LEMMA': 'model'}]
원본 주소 "https://wiki.mathnt.net/index.php?title=푸앵카레_상반평면_모델&oldid=52549"