로바체프스키 함수
개요
- 다이로그 함수(dilogarithm )의 변종으로 이해할 수 있다
- 로바체프스키 함수의 정의\[\Lambda(\theta)=-\int_0^{\theta} \ln |2\sin t| \,dt=\frac{1}{2}\sum_{n=1}^{\infty}\frac{\sin (2n\theta)}{n^2}\]
- 로바체프스키 함수는 쌍곡기하학의 연구에서 등장하였으며, 3차원 쌍곡다양체의 부피를 표현하는데 유용하다
- 클라우센 함수(Clausen function) 와의 관계\[\operatorname{Cl}_2(2\theta)=2\Lambda(\theta)\]
다이로그 함수와의 관계
- 다이로그 함수(dilogarithm)는 복소수 \(|z|<1\)에 대하여 다음과 같이 정의됨
\[\operatorname{Li}_2(z)= \sum_{n=1}^\infty {z^n \over n^2}\]
- \(|z|\leq 1\) 에서 고르게 수렴하는 급수이므로, \(|z|\leq 1\)에서 연속
- \(z=e^{2i\theta}\), \(0 \leq \theta \leq \pi\) 일 때, \[\operatorname{Li}_2(e^{2i\theta})= \sum_{n=1}^\infty \frac{e^{2in\theta}}{n^2}=\sum_{n=1}^\infty \frac{\cos 2n\theta}{n^2}+i\sum_{n=1}^\infty \frac{\sin 2n\theta}{n^2}\]
- 따라서 \(0 \leq \theta \leq \pi\) 일 때, \[\mathfrak{I}(\operatorname{Li}_2(e^{2i\theta}))=\sum_{n=1}^\infty \frac{\sin 2n\theta}{n^2}=2\Lambda(\theta)\]
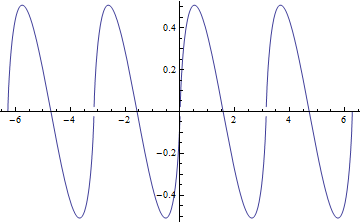
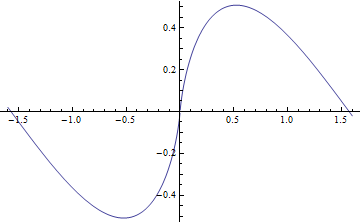
그래프
- \(\Lambda(\theta)\)는 기함수이고, \(\pi\) 를 주기로 가짐
- \(\theta=\pi/6+n\pi\)일 때 최대값을 가진다
멱급수 전개
- \(0 < \theta <\pi\) 일 때,
\[\Lambda(\theta)=\theta-\theta \log(2\theta)+2\theta\sum_{n=1}^{\infty}\frac{|B_{2n}|}{2n}\frac{(2\theta)^{2n}}{(2n+1)!}\] 여기서 \(B_{2n}\)은 베르누이 수
덧셈공식
- 예
\[ \Lambda (2\theta )=2 \left(\Lambda (\theta )+\Lambda (\theta +\frac{\pi }{2})\right) \] \[ \Lambda (3\theta )=3 \left(\Lambda (\theta )+\Lambda (\theta +\frac{\pi }{3})+\Lambda (\theta +\frac{2 \pi }{3})\right) \]
- 정리
자연수 \(n\)에 대하여 다음이 성립한다 \[ \Lambda(n\theta)=n\sum_{k=0}^{n-1}\Lambda(\theta+\frac{k\pi}{n}) \]
- 증명
다음을 이용하자 \[2\sin n\theta =\prod_{k=0}^{n-1}2\sin(\theta+\frac{k\pi}{n})\] 양변의 절대값에 로그를 취하여 양변을 적분하면, 적당한 상수 C에 대하여,다음을 얻는다 \[\frac{1}{n}\Lambda(n\theta)=\sum_{k=0}^{n-1}\Lambda(\theta+\frac{k\pi}{n})+C \label{feq} \] 이제 \(C=0\)임을 보이면 된다. \(n=2\)인 경우를 생각하자 \[\frac{1}{2}\Lambda(2\theta)=\Lambda(\theta)+\Lambda(\theta+\frac{\pi}{2})+C\] \(\theta=\frac{\pi}{2}\) 이면, \[\frac{1}{2}\Lambda(\pi)=\Lambda(\frac{\pi}{2})+\Lambda(\pi)+C\] \(\theta=0\) 이면, \[\frac{1}{2}\Lambda(0)=\Lambda(0)+\Lambda(\frac{\pi}{2})+C\] 두 식으로부터 \[\Lambda(\pi)=\Lambda(0)\]을 얻는다. 한편, \(\Lambda'(\theta)=- \ln |2\sin t|\) 는 \(\pi\) 를 주기로 가지므로, \(\Lambda(\theta)\) 역시 \(\pi\)를 주기로 갖는 함수가 된다. 즉 \[\Lambda(\theta+\pi)=\Lambda(\theta)\label{per}\] 이제 \ref{feq}에 기함수의 성질 \(\Lambda(-\theta)=-\Lambda(\theta)\)과 \ref{per}를 적용하여, \(C=0\)을 얻는다. ■
3차원 쌍곡기하학과의 관계
- 이면각이 \(\alpha, \beta, \gamma\)로 주어진 ideal tetrahedron \(T\)에 대하여, 다음이 성립한다
- \(\alpha+\beta+\gamma=\pi\)
- \(\operatorname{Vol}(T)=\Lambda(\alpha)+\Lambda(\beta)+\Lambda(\gamma)\)
- 이면각 (dihedral angles) : 주어진 모서리를 공유하는 두 면이 이루는 각
special values
- \(2\Lambda(\frac{\pi}{6})=3\Lambda(\frac{\pi}{3})=\operatorname{Cl}_2(\frac{\pi}{3})\)
- 이상 쌍곡 정사면체(ideal regular tetrahedron)의 부피
- http://mathworld.wolfram.com/GiesekingsConstant.html
- \(6\Lambda(\frac{\pi}{3})=2.0298832128193072500\cdots\)
- figure-eight 매듭 K에 의해 정의되는 3차원 쌍곡다양체 \(S^3-K\)의 부피
- \(2\Lambda(\frac{\pi}{4})+\Lambda(\frac{\pi}{2})=0.915965594\cdots\)는 카탈란 상수
역사
메모
관련된 항목들
매스매티카 파일 및 계산 리소스
관련논문
- Colin C. Adams The Newest Inductee in the Number Hall of Fame, Mathematics Magazine, Vol. 71, No. 5 (Dec., 1998), pp. 341-349
- John W. Milnor Hyperbolic geometry: The first 150 years, Journal: Bull. Amer. Math. Soc. 6 (1982), 9-24.
관련도서
- John G. Ratcliffe Foundations of hyperbolic manifolds
- Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century., Wellesley, MA: A K Peters, pp. 89-90, 2003.
- W. Thurston The Geometry and Topology of Three-Manifolds
- Chapter 7 (pdf)