2016학년도 대학수학능력시험 수학 B형 29번
개요
- 2016학년도 대학수학능력시험 수학 B형 29번 문제에 대하여, 실험수학 (experimental mathematics) 적 접근을 시도함
- 경험과학으로서의 수학을 소개하는 에세이
- 문제풀이의 4단계 전략
- 매개화를 이용하여 문제를 실험이 가능한 형태로 만들기
- 임의 추출을 이용한 실험을 수행하여 근사값 찾기
- 수치해석적 방법으로 더 정확한 근사값 찾기
- PSLQ 알고리즘을 적용하여 정확한 답을 찾기
문제의 이해
주어진 문제는 다음과 같다
좌표공간의 두 점 \(A(2,\sqrt{2},\sqrt{3})\) , \(B(1,-\sqrt{2},2 \sqrt{3})\) 에 대하여 점 \(P\) 는 다음 조건을 만족시킨다.
(가) \(|\overrightarrow{AP}|=1\)
(나) \(\overrightarrow{AP}\)와 \(\overrightarrow{AB}\)가 이루는 각의 크기는 \(\frac{\pi}{6}\)이다.
중심이 원점이고 반지름의 길이가 1인 구 위의 점 \(Q\)에 대하여 \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)의 최댓값이 \(a+b\sqrt{33}\)이다. \(16(a^2+b^2)\)의 값을 구하시오. (단, \(a,b\)는 유리수이다.)
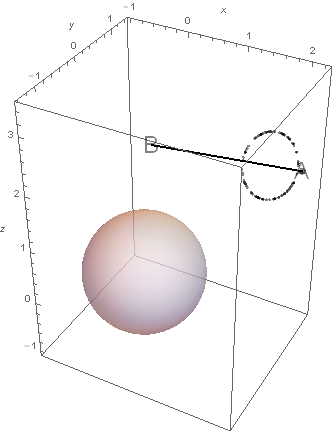
문제의 조건을 만족시키는 점 \(P\)는 위 그림의 원위에, \(Q\)는 단위구면 위에 놓여 있다. 이러한 조건 위에서 \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)의 값을 최대로 만들려고 한다.
여기서는 \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)의 최대값을 찾기 위해서, \(P\)와 \(Q\)를 임의로 뽑아내가면서, 그 값이 얼마나 커질 수 있는지에 대한 실험을 수행할 것이다.
원과 구면의 매개화
실험을 수행하기 위해서 \(P\)와 \(Q\)가 놓인 원과 구면을 매개화하자.
벡터의 내적과 외적에 대한 계산을 성실하게 수행하면 (물론 컴퓨터가 했다), \(P\)는 다음과 같은 원위에 놓여 있음을 알 수 있다. \[ P(t):=\left(\sqrt{\frac{3}{22}} \sin (t)+\frac{7 \cos (t)}{4 \sqrt{33}}+\frac{7}{4},-\frac{1}{2} \sqrt{\frac{3}{11}} \sin (t)+\frac{\cos (t)}{\sqrt{66}}+\frac{1}{\sqrt{2}},\frac{1}{44} \left(-2 \sqrt{22} \sin (t)+5 \sqrt{11} \cos (t)+55 \sqrt{3}\right) \right),\quad 0\leq t\leq 2\pi \label{PP} \]
단위구면은 구면좌표계를 이용하여 매개화할 수 있다. \[ Q(u,v):=\left(\cos u \sin v, \sin u \sin v, \cos v \right),\quad 0\leq u\leq 2\pi,0\leq v\leq\pi \label{QQ} \]
임의 추출을 이용한 실험
이제 컴퓨터를 이용하여 \(0\leq t\leq 2\pi,0\leq u\leq 2\pi,0\leq v\leq\pi\)를 만족하는 \((t,u,v)\)를 임의로 뽑아낸 뒤, \ref{PP}와 \ref{QQ}를 이용하여, \(P=P(t)\)와 \(Q=Q(u,v)\)를 구하고, \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)의 값을 구하자.
이를 백만번 시행하면서 전보다 더 큰 \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)의 값이 얻어질 때마다 이를 기록하자. 아래는 \(n\)번째 임의 추출에서 얻은 값 \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)과 \((t,u,v)\)의 표이다.
\[ \begin{array}{c|c|c} n & \overrightarrow{AP}\cdot \overrightarrow{AQ} & (t,u,v) \\ \hline 1 & 1.90334 & \{3.30047,2.08294,0.964364\} \\ 7 & 2.22899 & \{4.09651,2.8632,0.706553\} \\ 10 & 2.26728 & \{3.43351,4.16351,2.86169\} \\ 12 & 2.56336 & \{3.46444,3.90584,0.325815\} \\ 37 & 2.69629 & \{2.94468,3.36154,0.925869\} \\ 44 & 2.75229 & \{2.92377,5.14198,1.36891\} \\ 55 & 2.77746 & \{3.65922,3.5053,1.8994\} \\ 120 & 2.79647 & \{2.57083,4.29973,1.00076\} \\ 134 & 2.99473 & \{2.90661,4.08459,2.09397\} \\ 432 & 3.15013 & \{3.28658,4.25869,1.42484\} \\ 680 & 3.16119 & \{3.19468,3.89187,1.44537\} \\ 6695 & 3.17031 & \{3.08166,4.22474,1.6721\} \\ 9331 & 3.17362 & \{3.2183,3.98487,1.57295\} \\ 25934 & 3.17667 & \{3.19106,3.98259,1.54103\} \\ 67319 & 3.17772 & \{3.10662,4.02173,1.48524\} \\ 82935 & 3.18138 & \{3.06238,4.17261,1.51169\} \\ 160703 & 3.18452 & \{3.11131,4.16613,1.48792\} \\ 266823 & 3.18483 & \{3.16744,4.1446,1.53316\} \\ 353596 & 3.18553 & \{3.14674,4.10179,1.4851\} \\ 556290 & 3.18614 & \{3.14195,4.12252,1.51449\} \\ \end{array} \]
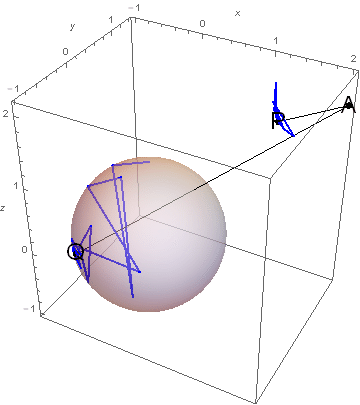
표에 해당하는 \(P\)와 \(Q\)의 위치가 어떻게 변하는지를 아래의 그림에서 관찰할 수 있다.
이 실험이 말해주는 것은 분명하다. \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)의 값을 최대로 만드는 쌍 \((P,Q)\)는 유일하게 존재하며, 그 값은 3.18 언저리이다.
내적의 최대값 찾기
매스매티카의 명령어 NMaximize를 이용하면, \(0\leq t\leq 2\pi,0\leq u\leq 2\pi,0\leq v\leq\pi\)일 때, 3변수 함수 \(\overrightarrow{AP(t)}\cdot\overrightarrow{AQ(u,v)}\)의 수치화된 최대값을 찾을 수 있는데, 이는 3.1861406616345071649626528670547323295550661144957 이다.
이는 위에서 실행한 실험의 결과에 부합한다. 따라서 이제 \(\overrightarrow{AP}\cdot\overrightarrow{AQ}\)의 최대값에 대한 확신을 가질 수 있다.
PSLQ 알고리즘의 적용
이제 위에서 얻은 값을 \(\alpha=3.1861406616345071649626528670547323295550661144957\)라 두자.
문제에서는 \(\overrightarrow{AP}\cdot \overrightarrow{AQ}\)의 최대값이 \(a+b\sqrt{33}, a,b\in \mathbb{Q}\)꼴이라고 하였으므로, 만약에 \(a+b\sqrt{33}=\alpha\)의 관계가 성립한다면, 적당한 정수 \(p,q,r\)가 존재하여 \(p+q \sqrt{33}+r \alpha=0\)이 성립해야 한다.
이러한 상황에서 유용한 실험수학의 알고리즘이 바로 PSLQ 알고리즘이다. 이는 주어진 여러개의 실수 사이에 정수 계수를 이용한 선형 결합 관계가 존재하는지를 찾는데 이용된다. PSLQ 알고리즘을 적용하면, \((p,q,r)=(7,1,-4)\)를 얻는다. 즉 \(7+\sqrt{33}-4 \alpha=0\)가 성립할 개연성이 높다는 것이다.
따라서 \((a,b)=(7,1)/4\)이고, 문제의 답은 50이 된다.
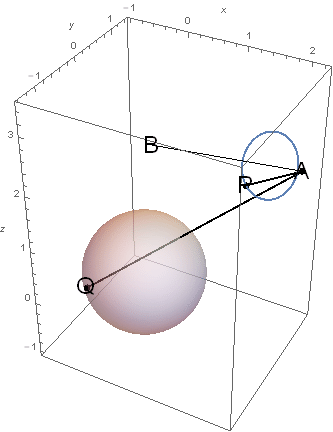
참고로, 이렇게 내적의 값을 최대로 만드는 \(P\)와 \(Q\)의 위치는 다음과 같다 \[ \begin{aligned} P & =\left(\frac{7}{4}-\frac{7}{4 \sqrt{33}},\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{66}},\frac{5 \sqrt{3}}{4}-\frac{5}{4 \sqrt{11}}\right) \\ Q & =\left(-\frac{1}{4}-\frac{7}{4 \sqrt{33}},-\sqrt{\frac{17}{33}+\frac{1}{\sqrt{33}}},\frac{\sqrt{3}}{4}-\frac{5}{4 \sqrt{11}}\right) \end{aligned} \]
연분수의 활용
- \(\alpha=3.1861406616345071649626528670547323295550661144957\)가 실이차수체의 원소이므로 연분수 전개를 이용할수도 있다
\[ \alpha=3+\frac{1}{5+\frac{1}{2+\frac{1}{1+\frac{1}{2+\frac{1}{5+\frac{1}{2+\frac{1}{1+\frac{1}{2+\frac{1}{\cdots}}}}}}}}}=[3;5,2,1,2,5,2,1,2,\cdots] \]
- \(\alpha=3+\beta\)로 두면, \(\beta=[0;5,2,1,2+\beta]=\frac{3 \beta +8}{16 \beta +43}\)가 성립하고, 따라서
\[ \beta=\frac{1}{4} \left(\sqrt{33}-5\right) \]
관련된 항목들
매스매티카 파일 및 계산 리소스
리뷰, 에세이, 강의노트
- Bailey, David H., and Jonathan M. Borwein. "Experimental mathematics: Examples, methods and implications." Notices of the AMS 52.5 (2005): 502-514. http://www.ams.org/notices/200505/fea-borwein.pdf