"드 무아브르의 정리, 복소수와 정다각형"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) |
||
| 1번째 줄: | 1번째 줄: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==개요== | ==개요== | ||
| 65번째 줄: | 55번째 줄: | ||
* [[복소수]] | * [[복소수]] | ||
* [[추상대수학]] | * [[추상대수학]] | ||
| − | |||
* [[복소함수론]] | * [[복소함수론]] | ||
2013년 3월 3일 (일) 02:14 판
개요
(정리) 드 무아브르
\((\cos \theta + i \sin \theta)^n=\cos n\theta + i \sin n\theta\)
여기서 \(\theta\) 는 임의의 실수, \(n\) 은 임의의 정수
증명
- 수학적 귀납법
오일러의 정리를 통한 증명
- 오일러의 공식
- 복소지수함수 \(e^{i\theta}=\cos \theta+ i\sin \theta\) 의 성질에서 자연스럽게 유도
\((\cos \theta+ i\sin \theta)^n=(e^{i\theta})^n=e^{in\theta}= \cos n\theta+ i\sin n\theta\)
정다각형과의 관계
- \(z^n=1\) 를 만족시키는 복소수 방정식을 풀면, n개의 해는 복소평면에서 정n각형의 꼭지점이 된다.
방정식을 풀기 위해, \(z=\cos \theta + i \sin \theta\) 로 두고 드 무아브르 정리를 적용하자.\[(\cos \theta + i \sin \theta)^n=\cos n\theta + i \sin n\theta=1\]\[\theta=\frac{2k\pi}{n}, k=0,1,\cdots,n-1\]
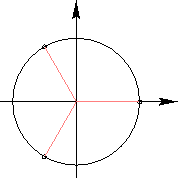
- \(z^3=1\) 의 해는, \(1,\frac{-1+\sqrt{-3}}{2}, \frac{-1-\sqrt{-3}}{2}\) 세 개가 있다. 이를 복소평면에 점으로 나타내면, 다음과 같이 정삼각형의 꼭지점을 이룬다.
많이 나오는 질문
관련된 고교수학 또는 대학수학
관련된 항목들
- 정다각형의 작도
- 정오각형
- 가우스와 정17각형의 작도
- 수학사 연표
- [[오일러의 공식 e^{iπ}+1=0|오일러의 공식]]
- 정규분포와 중심극한정리
사전형태의 자료
- http://ko.wikipedia.org/wiki/복소수
- http://en.wikipedia.org/wiki/De_Moivre
- http://en.wikipedia.org/wiki/De_Moivre's_formula