축구공의 수학

수학노트
둘러보기로 가기 검색하러 가기

개요

  • 축구공에는 재미있는 수학적 사실들이 담겨있음.
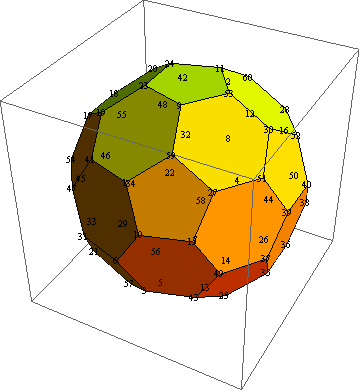
  • 깎은 정이십면체 (truncated icosahedron)
  • 정오각형 12개, 정육각형 20개로 구성
  • 60개의 꼭지점
  • 90개의 모서리

축구공의 수학1.png


데카르트 정리의 응용

  • 볼록다면체에 대한 데카르트 정리는 위상적인 성질을 반영하는 것이기 때문에, 사실은 꼭 정다면체뿐만이 아니라, 축구공과 같은 일반적인 (볼록)다면체에서도 성립함.
    • 볼록다면체의 각 꼭지점에서의 결손각을 모두 더하면 \(4\pi\)가 된다

축구공의 꼭지점의 개수를 세는 법

  • 모든 꼭지점이 똑같이 생겼다는 사실을 확인.
  • 한 점에는 정오각형 하나, 정육각형 두개가 만나고 있다는 사실을 재빠르게 간파한 다음,
  • 정오각형 한점 내각 = 108도, 정육각형 한점 내각 = 120도
  • 따라서 축구공 한 점에서의 결손각 크기 = 360도 -(108도+120도+120도) = 12도,이는 \(\pi/15\) 라디안에 해당한다
  • 데카르트 정리를 이용하면 꼭지점의 개수는 다음과 같다

\[ 4\pi/(\pi/15) = 60 \]

  • 그러므로 축구공에는 꼭지점이 60개 있음.



메모



역사


관련된 항목들



관련된 고교수학 또는 대학수학


매스매티카 파일 및 계산 리소스


사전형태의 자료


리뷰, 에세이, 강의노트

관련논문

  • Kostant, B. 1995. “Structure of the Truncated Icosahedron (e.g.\ Fullerene or \(\rm C_60\), Viral Coatings) and a \(60\)-Element Conjugacy Class in \(\rm PSL(2,11)\).” Selecta Mathematica. New Series 1 (1): 163–195. doi:10.1007/BF01614076.
  • Kostant, Bertram. 1994. “Structure of the Truncated Icosahedron (such as Fullerene or Viral Coatings) and a \(60\)-Element Conjugacy Class in \(\rm PSl(2,11)\).” Proceedings of the National Academy of Sciences of the United States of America 91 (24): 11714–11717. doi:10.1073/pnas.91.24.11714.
  • Chung, Fan R. K., Bertram Kostant, and Shlomo Sternberg. 1994. “Groups and the Buckyball.” In Lie Theory and Geometry, 123:97–126. Progr. Math. Boston, MA: Birkhäuser Boston. http://www.ams.org/mathscinet-getitem?mr=1327532.
  • James, Gordon. 1994. “The Representation Theory for Buckminsterfullerene.” Journal of Algebra 167 (3): 803–820. doi:10.1006/jabr.1994.1213.


관련기사

원본 주소 "https://wiki.mathnt.net/index.php?title=축구공의_수학&oldid=48247"