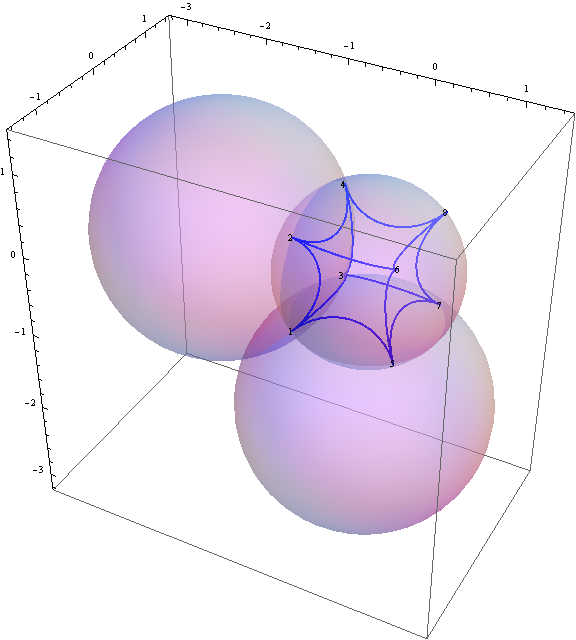
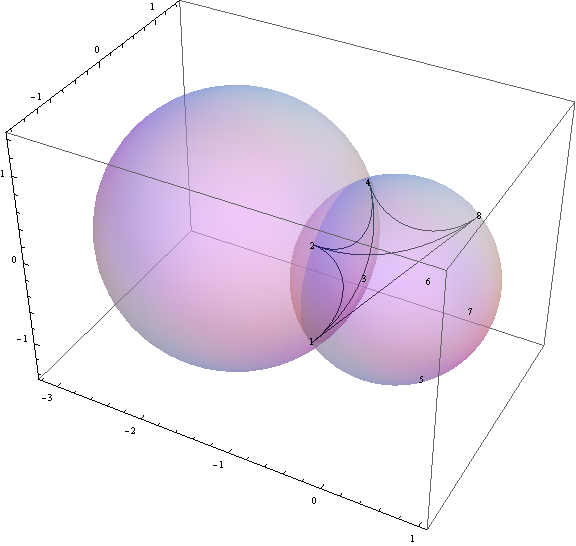
쌍곡 정육면체

개요

• 3차원 푸앵카레 unit ball 모델에서의 쌍곡 정육면체
• 꼭지점들이 unit ball에 놓여 있는 경우 (ideal hyperbolic regular cube)

• 세 이면각이 각각 \(\frac{\pi }{2},\frac{\pi }{3},\frac{\pi }{6}\)인 사면체

쌍곡다양체로서의 부피

• \(15 \Lambda \left(\frac{\pi }{3}\right)=6 \left(\Lambda \left(\frac{\pi }{6}\right)+\Lambda \left(\frac{\pi }{3}\right)+\Lambda \left(\frac{\pi }{2}\right)\right)=5.0747080320482681251\cdots\)
• 여기서 \(\Lambda\)는 로바체프스키 함수

관련된 항목들

• 쌍곡 정십이면체
• 정다면체
• 로바체프스키 함수

매스매티카 파일 및 계산 리소스

• https://docs.google.com/file/d/0B8XXo8Tve1cxcUtXNkVWQWt1R3M/edit
• http://www.wolframalpha.com/input/?i=5.074708032048268125