"피보나치 수열"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
|||
| (사용자 2명의 중간 판 36개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | < | + | ==개요== |
| + | * 수열 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... | ||
| + | * 앞에 있는 두 수를 더하여, 다음의 수를 얻는다 | ||
| + | * 점화식을 이용한 정의 | ||
| + | :<math>F_{n+2}=F_{n+1}+F_{n}, \\ | ||
| + | F_0=1,F_1=1</math> | ||
| + | * [[상수계수 선형점화식]]의 예이다 | ||
| + | * [[루카스 수열]]의 예이다 | ||
| + | * 인접한 두 수열의 비는 [[황금비]]로 수렴 | ||
| + | :<math>\lim_{n\to\infty}\frac{F_{n+1}}{F_n}=\varphi=\frac{1+\sqrt5}{2}=1.61803398874989\cdots</math> | ||
| − | + | ==피보나치 수열의 일반항== | |
| − | + | * [[생성함수]]를 이용하여 얻을 수 있다 | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ;정리 | |
| + | 피보나치 수열의 생성함수는 다음과 같이 주어진다 | ||
| + | :<math>s(x)=\sum_{k=0}^{\infty} F_k x^k=\frac{1}{1-x-x^2}\label{s}</math> | ||
| − | + | ;증명 | |
| − | < | + | 점화식을 이용하여 다음을 얻는다 |
| + | :<math>\begin{align} s(x) &= \sum_{k=0}^{\infty} F_k x^k \\ &= F_0 + F_1x + \sum_{k=2}^{\infty} \left( F_{k-1} + F_{k-2} \right) x^k \\ &= F_0 + F_1x + \sum_{k=2}^{\infty} F_{k-1} x^k + \sum_{k=2}^{\infty} F_{k-2} x^k \\ &= 1+ x + x(\sum_{k=0}^{\infty} F_k x^k-1) + x^2\sum_{k=0}^{\infty} F_k x^k \\ &= 1+ x s(x) + x^2 s(x) \end{align}</math> | ||
| − | |||
| − | <math> | + | ;따름정리 |
| + | 피보나치수열의 일반항은 다음과 같다 | ||
| + | :<math> | ||
| + | F_n= \frac{\left(\frac{1}{2} \left(1+\sqrt{5}\right)\right)^{n+1}-\left(\frac{1}{2} \left(1-\sqrt{5}\right)\right)^{n+1}}{\sqrt{5}} | ||
| + | </math> | ||
| − | + | \ref{s}의 우변을 부분분수로 분해하여 쓰면 된다. | |
| − | <math> | + | ==여러가지 성질들== |
| + | * <math>F_{n+1}F_{n-1} - F_n^2=(-1)^{n-1}</math> | ||
| + | * 위의 성질들을 이용하면, 다음과 같은 식들을 얻을 수 있음. | ||
| + | :<math>\sum_{n=0}^{\infty}\frac{(-1)^{n+1}}{F_nF_{n+1}}=\varphi-1</math> | ||
| + | :<math>\prod_{n=1}^{\infty}(1+\frac{(-1)^{n-1}}{F_n^2})=\varphi</math> | ||
| + | * <math>\gcd(F_m,F_n)=F_{\gcd(m,n)}</math>에 대해서는 [[피보나치 수열의 나눗셈 성질]] 항목 참조 | ||
| + | * 피보나치 수열을 자연수 n으로 나눈 나머지로 정의된 수열은 주기성을 가진다 | ||
| + | ** [[피보나치 수열과 합동식]] 항목 참조 | ||
| − | + | ==황금비와 피보나치 수열== | |
| − | + | [[파일:2252978-goldenrectangle.jpg]] | |
| − | + | ||
| − | + | ||
| − | + | ==자연과 피보나치 수열== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[http://www.mathematicianspictures.com/images_275/275_FI_CREDITS_75PCMATHPICS.jpg ] | [http://www.mathematicianspictures.com/images_275/275_FI_CREDITS_75PCMATHPICS.jpg ] | ||
| − | [ | + | [[파일:2252978-275_FI_MATH_FIB_NAUT_2030_P.jpg]] |
| − | |||
| − | [ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[파일:2252978-fb_r003b.jpg]] | |
| − | |||
| − | + | ||
| + | * [http://www.boutiqueacademia.com/products/Fibonacci-Earrings.html 피보나치 귀걸이] | ||
| − | + | ==메모== | |
| + | * [[파일:2252978-전체화면 캡처 2009-03-01 오후 123738.jpg]] | ||
| + | * [http://www.math.temple.edu/%7Erenault/fibonacci/fib.html http://www.math.temple.edu/~renault/fibonacci/fib.html] | ||
| + | * [[Phyllotaxis]] | ||
| + | * Kotesovec, Vaclav. “Asymptotics of the Euler Transform of Fibonacci Numbers.” arXiv:1508.01796 [math], August 7, 2015. http://arxiv.org/abs/1508.01796. | ||
| − | + | ==관련된 항목들== | |
| − | + | * [[피보나치 수열의 짝수항]] | |
| − | * [ | ||
| − | |||
| − | + | ==매스매티카 파일 및 계산 리소스== | |
| + | * https://docs.google.com/file/d/0B8XXo8Tve1cxYTBlNHdVdFdDZEk/edit | ||
| − | + | [[분류:수열]] | |
| − | |||
| − | |||
| − | |||
2020년 12월 28일 (월) 04:10 기준 최신판
개요
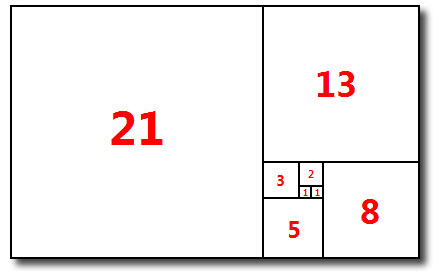
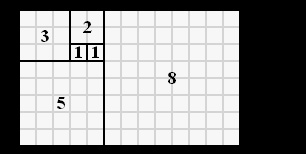
- 수열 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
- 앞에 있는 두 수를 더하여, 다음의 수를 얻는다
- 점화식을 이용한 정의
\[F_{n+2}=F_{n+1}+F_{n}, \\ F_0=1,F_1=1\]
- 상수계수 선형점화식의 예이다
- 루카스 수열의 예이다
- 인접한 두 수열의 비는 황금비로 수렴
\[\lim_{n\to\infty}\frac{F_{n+1}}{F_n}=\varphi=\frac{1+\sqrt5}{2}=1.61803398874989\cdots\]
피보나치 수열의 일반항
- 생성함수를 이용하여 얻을 수 있다
- 정리
피보나치 수열의 생성함수는 다음과 같이 주어진다 \[s(x)=\sum_{k=0}^{\infty} F_k x^k=\frac{1}{1-x-x^2}\label{s}\]
- 증명
점화식을 이용하여 다음을 얻는다 \[\begin{align} s(x) &= \sum_{k=0}^{\infty} F_k x^k \\ &= F_0 + F_1x + \sum_{k=2}^{\infty} \left( F_{k-1} + F_{k-2} \right) x^k \\ &= F_0 + F_1x + \sum_{k=2}^{\infty} F_{k-1} x^k + \sum_{k=2}^{\infty} F_{k-2} x^k \\ &= 1+ x + x(\sum_{k=0}^{\infty} F_k x^k-1) + x^2\sum_{k=0}^{\infty} F_k x^k \\ &= 1+ x s(x) + x^2 s(x) \end{align}\]
- 따름정리
피보나치수열의 일반항은 다음과 같다 \[ F_n= \frac{\left(\frac{1}{2} \left(1+\sqrt{5}\right)\right)^{n+1}-\left(\frac{1}{2} \left(1-\sqrt{5}\right)\right)^{n+1}}{\sqrt{5}} \]
\ref{s}의 우변을 부분분수로 분해하여 쓰면 된다.
여러가지 성질들
- \(F_{n+1}F_{n-1} - F_n^2=(-1)^{n-1}\)
- 위의 성질들을 이용하면, 다음과 같은 식들을 얻을 수 있음.
\[\sum_{n=0}^{\infty}\frac{(-1)^{n+1}}{F_nF_{n+1}}=\varphi-1\] \[\prod_{n=1}^{\infty}(1+\frac{(-1)^{n-1}}{F_n^2})=\varphi\]
- \(\gcd(F_m,F_n)=F_{\gcd(m,n)}\)에 대해서는 피보나치 수열의 나눗셈 성질 항목 참조
- 피보나치 수열을 자연수 n으로 나눈 나머지로 정의된 수열은 주기성을 가진다
- 피보나치 수열과 합동식 항목 참조
황금비와 피보나치 수열
자연과 피보나치 수열
메모
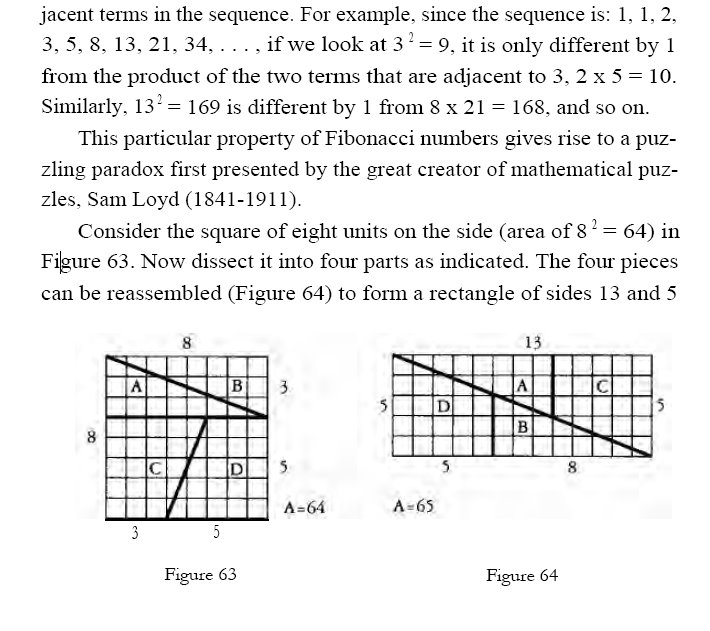
- http://www.math.temple.edu/~renault/fibonacci/fib.html
- Phyllotaxis
- Kotesovec, Vaclav. “Asymptotics of the Euler Transform of Fibonacci Numbers.” arXiv:1508.01796 [math], August 7, 2015. http://arxiv.org/abs/1508.01796.
관련된 항목들