고교생도 이해할 수 있는 군론 입문
개요
- {차렷, 좌향좌, 우향우, 뒤로돌아}의 수학적 구조를 통해 군론을 소개함
군이란 무엇인가
요즘 어떻게 군론을 소개하면 좋을까 고민을 좀 하고 있었는데, 우연히 마틴 가드너의 책 ‘The Last Recreations: Hydras, Eggs, and Other Mathematical Mystifications‘ 을 넘겨 보다가 좋은 걸 배웠다.
군, 群, group 이란 무엇인가? 오늘은 몇 개의 군대 용어를 사용하여, 군론을 소개하려 한다. 다만 주의할 것은, 수학용어 군은 무리 군 群으로 군대와는 관계가 없으니 혼동이 없기를…
지금 교관과 훈련병이 제식훈련 중이다. 훈련병은 차렷자세로 교관을 바라보고 있다. 교관은 곧 훈련병에게 네 가지의 명령을 막 섞어서 뺑뺑이를 돌리기 시작한다. 그 네 가지의 명령이란 다음과 같다.
차렷, 좌향좌, 우향우, 뒤로돌아
지금부터 이 네 개 명령들의 모임, {차렷, 좌향좌, 우향우, 뒤로돌아} 가 가진 수학적인 구조에 대해 살펴볼까 한다. 무진장 쉽기 때문에, 군인도 이해할 수 있다고 본다. 결론을 미리 말하자면, 이 명령들의 모임은 ‘크기가 4인 군‘의 구조를 갖는다.
관찰0
교관이 두 개의 명령을 내렸다. 그렇다면, 그 두 개의 명령은 어떤 하나의 명령과 똑같은 결과를 준다는 것을 알 수 있다. 예를 들자면, 좌향좌.좌향좌 = 뒤로돌아. 뒤로돌아.좌향좌=우향우 가 성립하는 것이다 모든 두 개의 명령은 어떤 하나의 명령과 동일하게 볼 수 있다. 수학적으로 말하자면, 명령들 사이에는 일종의 연산이 가능한 것이다.
(물론 결과적으로 그렇다는 것이지, 훈련병이 좌향좌 두번들었다고 가만히 있다가 뒤로돌아 한번하면, 큰일이 나겠죠)
이 연산의 표를 만드는 것도 가능하다. 맨 왼쪽줄의 명령이 먼저 오고, 그 다음에 맨 위쪽줄의 명령이 온다고 하면, 연산표는 다음과 같다.
| . | 차렷 | 좌향좌 | 뒤로돌아 | 우향우 |
|---|---|---|---|---|
| 차렷 | 차렷 | 좌향좌 | 뒤로돌아 | 우향우 |
| 좌향좌 | 좌향좌 | 뒤로돌아 | 우향우 | 차렷 |
| 뒤로돌아 | 뒤로돌아 | 우향우 | 차렷 | 좌향좌 |
| 우향우 | 우향우 | 차렷 | 좌향좌 | 뒤로돌아 |
관찰1
‘차렷’이 명령들 사이사이에 들어가 있어도 이것은 결과적으로 아무런 변화를 가져오지 않는다.
관찰2
모든 명령은, 다른 명령을 통해 그 명령을 내리기 전 상태로 되돌릴 수 있다. 예를 들자면, 좌향좌라고 방금 말했다면 우향우를 통해 상태를 되돌릴 수 있다. 방금 우향우라고 했다면, 좌향좌로 상태를 되돌릴 수 있다.
관찰3
명령들의 연산에는 결합법칙이 성립한다. 다시 말하자면, (a.b).c = a.(b.c) 가 성립한다. 예를 들어, a= 좌향좌, b= 뒤로돌아, c=우향우 라고 해보자.
(a.b).c = (좌향좌.뒤로돌아).우향우 = (우향우).우향우 = 뒤로돌아 a.(b.c) = 좌향좌.(뒤로돌아.우향우) = 좌향좌.(좌향좌) = 뒤로돌아
a,b,c에 어느 명령 셋을 가져오더라도 이러한 등식은 성립한다. 왜 이러한 결합법칙이 성립하는 것일까? 이 질문이 사실 군을 공부하는데 있어 가장 중요한 질문이다. 이에 대한 설명은 아래에 제시하겠다.
군이란 무엇인가
이 예를 잘 이해했다면, 이제 ‘군’이란 무엇인가라는 질문에 답을 하기가 한결 수월해진다.
0. 이항연산이 가능한 집합으로, 즉 두 개의 원소 사이에 연산이 가능하여 그 둘의 연산이 주는 결과가 그 집합에 다시 들어있다 (우리의 경우에는 {차렷, 좌향좌, 우향우, 뒤로돌아} )
1. 연산에 대한 결합법칙이 성립 [ 예를 들자면, (좌향좌.뒤로돌아).우향우 = 좌향좌.(뒤로돌아.우향우) ]
2. 각 원소에 대하여 역원, 즉 그와 연산을 했을 때 항등원이 되는 원소가 존재(차렷의 역원은 차렷, 좌향좌의 역원은 우향우, 우향우의 역원은 좌향좌, 뒤로돌아의 역원은 뒤로돌아)
3. 그 집합에 연산에 대한 항등원이 존재 (’차렷’)
의 조건을 만족시킬때, 우리는 그 집합을 ‘군’이라 한다.
그러면 이제 다음 시간까지, 위의 관찰3에서 왜 결합법칙이 성립하는지를 곰곰이 생각해 보시길…
결합법칙
위에서는 {차렷, 좌향좌, 우향우, 뒤로돌아} 이라는 집합이 ‘군’이라는 수학적 구조를 이룬다는 것을 보였다. 그리고 결합법칙에 대한 설명을 따로 떼어두었다. 주어진 이항연산이 다음과 등식을 만족시킬때, 우리는 결합법칙이 성립한다고 말한다.
(a.b).c = a.(b.c)
{차렷, 좌향좌, 우향우, 뒤로돌아} 에 주어진 연산은 왜 결합법칙을 만족시키는 것일까? 이유는 간단하다. 이것들은 뺑뺑이를 돌고 있는 훈련병에게 주어지는 명령이기 때문이다! what??? ?@@?
(좌향좌.뒤로돌아).우향우 = 좌향좌.(뒤로돌아.우향우) 가 성립하는 이유는 지극히 당연한 것이다. (좌향좌.뒤로돌아).우향우 라는 명령이 연달아 내려왔다면, 훈련병은 그저 좌향좌, 뒤로돌아, 우향우 동작을 연달아 하면 그만이다. 좌향좌.(뒤로돌아.우향우) 라는 명령이 내려왔다면, 역시 좌향좌, 뒤로돌아, 우향우의 순서대로 움직이기만 하면 된다. 그러니 결합법칙이 성립하지 않을수가 없다!
(너무 당연한 것을 말하고 있으니, 오히려 더 혼란스러울 것 같기도 하다. 그러나 지금까지의 이야기들은 매우 중요한 것들이다. 여기까지의 내용을 잘 따라온 사람들은 군론에 대한 소개를 받았고 더 나아가 ‘군표현론’(group representation theory)의 철학까지 소개받고 있다.)
지금 여기 네 가지의 명령들로 구성된 집합이 있고 그에 따라 뺑뺑이를 도는 훈련병이 있다. 수학적으로 말하자면, group of transformations 이 있고, 그 각각의 transformation (즉 하나하나의 명령들) 에 따라서 변화하고 있는 대상(훈련병)이 있다. 개개의 transformation 사이의 연산이, 그저 대상에 주어진 명령들을 순서대로 행하는 것과 같다면, 이러한 연산은 당연히 결합법칙을 만족시킨다.
행렬의 곱셈과 결합법칙
지금까지의 당연하게만 들리는 이야기 속에 담긴 힘을 보여주기 위해, 행렬의 곱셈에 대해서 언급하고자 한다. 고등학교 수학과정에서 행렬이 등장하고, 행렬의 곱셈도 정의한다. 그리고 행렬의 곱셈은 결합법칙을 만족시킨다는 것도 교과서도 나온다. 그러나 왜 행렬의 곱셈이 결합법칙을 만족시키는지는 제대로 설명해 주지 않는다. 행렬의 곱셈은 정의부터 이상하지 않았는가? \[\mathbf{A} = \begin{pmatrix}<br/>a & b \\<br/>c & d \\ \end{pmatrix}, \mathbf{B} = \begin{pmatrix}<br/>e & f \\<br/>g & h \\ \end{pmatrix}\] 라고 한다면, 행렬의 곱셈은 \[\mathbf{AB} = \begin{pmatrix}<br/>ae+ bg & af+bh \\<br/>ce+dg & cf+dh \\ \end{pmatrix}\] 로 정의된다.
먼저 행렬의 곱셈은 왜 이렇게 괴상하게 정의된 것일까? 그 이유는 바로 하나하나의 행렬들은 함수이기 때문이다!
2차원 평면상의 점 (x,y)를 (ex+fy, gx+hy)로 보내주는 함수 f 가 있다. 그리고 또 다른 함수 g 가 있어 (x,y)를 (ax+by,cx+dy)로 보내준다고 하자. 그렇다면 함수 f와 g의 합성은 (x,y)를 어디로 보낼까?
계산을 해 보면 이렇다. \[ f : (x,y) \mapsto (ex+fy, gx+hy)\] \[ g : (ex+fy, gx+hy) \mapsto ( (ae+ bg)x+(af+bh)y, (ce+dg)x+(cf+dh)y )\]
이 결과를 가만히 잘 들여다 보면, 함수 f의 역할을 행렬 B가 할 수 있고, 함수 g의 역할을 행렬 A가 한다고 하면, 함수의 합성 \(g \circ f\) 의 역할은 행렬 AB 가 할 수 있다는 것을 알 수 있다.
행렬의 곱셈을 저리 괴상하게 정의한 이유는, 바로 행렬들을 함수로 보고 싶었기 때문이다! 이것이 바로 선형대수학 제일의 철학, ‘선형사상은 행렬과 같다’ 는 말이다. (사상 = 함수)
지금까지 한 얘기들을 모두 정리하면 이렇다. 여러개의 명령들이 있고, 그에 따라 뺑뺑이를 도는 훈련병이 있다면, 명령들 사이의 연산에서 결합법칙은 당연하게 성립한다.
각각의 2×2 행렬들을 하나하나의 명령들로 이해한다면, 뺑뺑이 도는 훈련병 역할을 2차원평면이 맡는다. 각각의 행렬들은 2차원 평면에 내려지는 명령들로 이해할 수 있다. 행렬 A,B이 있고, B,A 의 순서로 2차원평면상에 명령을 내릴 경우, 그 결과는 AB라는 행렬이 하는 명령과 동일하다.
그리고 세 개의 명령 A,B,C가 있어 C,B,A의 순서로 명령이 내려진다면, 그 명령은 행렬 ABC 가 하는 역할과 똑같다.
그러므로 행렬들의 곱셈은 결합법칙을 만족시킨다!!
\(A(BC)=(AB)C\)
행렬 세 개를 가지고 계산하지 않고 이런 결론을 내릴 수 있다는 것이 지금까지 길었던 이야기의 핵심이었다. 여기서 감동하지 않은 사람은 지금까지 이야기를 이미 알고 있었거나, 이해하지 못했거나 둘 중의 하나!!
다음 이야기는 ‘군론입문’시리즈의 마지막 편으로, 군론은 왜 ‘대칭‘을 이해하는 언어가 되는지를 말한다.
대칭의 언어
20세기 수학자 헤르만 바일이 쓴 ‘Symmetry‘라는 책이 있다. 교양을 위한 수학책이라 할 수 있지만, 내가 학부생 시절 학교 중앙도서관에서 빌려 읽은 이 책은 수학 섹션이 아닌 예술 섹션에 꽂혀 있었다. 그 책의 초반부에서 바일은 다음과 같이 말한다.
Symmetry is one of the ideas by which man through the ages has tried to comprehend and create order, beauty, and perfection. 대칭은 인류가 오랜 시간 동안, 그를 통해 질서, 미, 완벽함과 같은 것들을 이해하고 창조하기 위해 노력했던 관념 중의 하나이다.
국어사전은 대칭에 대하여 다음과 같이 말한다.
대칭 (對稱) [대ː-] 「명」 「1」『물』한 결정 입자를 다른 결정 입자에 반사시키거나 어떤 축을 중심으로 회전시켰을 때 다른 결정 입자와 포개지는 성질. ≒상칭(相稱). 「2」『미』균형을 위하여 중심선의 상하 또는 좌우를 같게 배치한 화면 구성. ≒균제(均齊)〔2〕˙대칭 구성˙좌우 상칭〔2〕.「3」『어』=제이 인칭. 「4」『수1』점˙선˙면 또는 그것들의 모임이 한 점˙직선˙평면을 사이에 두고 같은 거리에 마주 놓여 있는 일. 점인 경우에는 점대칭, 직선일 경우에는 선대칭, 평면일 경우에는 면대칭이라고 한다. ≒맞맞이˙맞섬.
누구나 대칭이란 말에 대한 어떠한 이해를 가지고 있을 것이다. 그리고 그것은 아마도 위의 국어사전과 비슷한 무언가를 포함할 것이다. 그러나 위의 사전은 무언가 부족하다. 각각의 항목에 대하여 비슷비슷한 말들을 사용하고 있지만, 하나로 명료하게 포괄하지를 못하고 있다. 도대체 대칭을 무엇이라 하는게 좋을까?
지금까지 내가 지니고 있는 가장 좋아하는 ‘대칭’에 대한 정의(?)는 이것이다.
변화 속의 불변
이 얼마나 아름답고 멋진 시적 표현인가? 모두 이 말을 위의 국어사전에 나온 설명에 어떻게 적용할 수 있을지 조금 시간을 두고 생각해 보길 바란다. 이에 따르자면, 어떤 대상이 ‘대칭성’을 가지고 있다는 것은 그 대상이 ‘변화 속의 불변성’을 가지고 있다는 말이다. 이러한 대칭의 정의는 대칭이라는 말에 연관된 두 가지 요소를 구분한다. 하나는 ‘변화’들, 다른 하나는 그 변화에 따라 ‘불변하는 대상’이다. 바로 이 지점에서 군론이 등장한다. 군이란 바로 어떤 불변성을 가진 대상에 대한 ‘변화’들의 모임인 것이다!
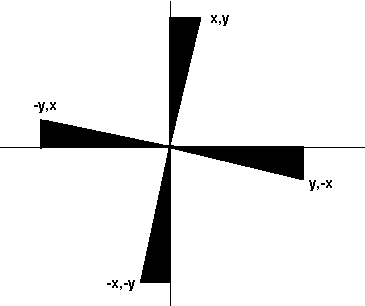
그렇다면 군을 소개하기 위해 예로 들었던, {차렷, 좌향좌, 우향우, 뒤로돌아}라는 군은 도대체 대칭과 어떤 관련이 있는 것일까? 그 명령들이 내려지고 있던 훈련병은 도대체 무슨 불변성을 가지고 있던 것인가? 사실 훈련병은 이야기를 쉽게 풀어나가기 위해 끌어들인 장치에 불과했고, 사실 본질은 바로 다음과 같은 그림이다.
더 유명한 것으로, 만자문 또는 Swastika 라고 불리는 다음과 같은 형상들이 있다.
위키에 따르면 swastika는 산스크리트어 기원으로 행운을 뜻하는 상징이라 한다. 나치만 없었어도, 상대하는데 아무런 거리낌이 없을 문양이었다. 어쨌든 헤르만 바일이 언급한 ‘질서, 미, 완벽함’같은 것들은, 아마도 대칭성이 가져오는 신비로움, 영적인 힘 같은 것들과도 연관이 있을 것이다.
저 문양들은 모두 다르게 생겼지만, {차렷, 좌향좌, 우향우, 뒤로돌아}라는 동일한 변화들의 모임에 의해 불변성을 갖는다. 또한 네 개의 복소수로 이루어진 군 \(\{1,i,-1,-i\}\)은 {차렷, 좌향좌, 우향우, 뒤로돌아} 와 동일한 수학적인 구조를 갖고 있다. 수학자들은 이렇게 이름만 다르지만 본질적으로 같은 군들을 추상화하여 모두 순환군 \(C_4\) (cyclic group of order 4) 라고 부른다. 이러한 방식으로 ‘군’의 개념은 이러한 사실상 달라 보이지만 똑같은 ‘대칭’을 분류하는데 있어, 강력한 언어를 제공해 주게 되는 것이다!
재미있는 사실
- 역사적으로 군론은 방정식의 근의 공식에 대한 질문에 답하는 과정에서 탄생함.
관련된 항목들
관련도서
관련된 고교수학 또는 대학수학
블로그
- 피타고라스의 창
메타데이터
위키데이터
- ID : Q83478
Spacy 패턴 목록
- [{'LEMMA': 'group'}]