정칠각형

개요

• 정칠각형에 관련된 여러 가지 수학적 주제의 이해

정칠각형 꼭지점의 평면좌표

• 정칠각형이 단위원에 내접하고 있고, 한 점의 좌표가 \((1,0)\)으로 주어진 경우
• 방정식 \(z^6 + z^5 + z^4 + z^3 + z^2 + z + 1 = 0\)은 다음과 같은 순서로 풀수 있음.
• 양변을 \(z^3\)으로 나누면, \(z^3+z^2+z+1+\frac{1}{z}+\frac{1}{z^2}+\frac{1}{z^3}=0\) 을 얻게됨.
• \(y=z+\frac{1}{z}\) 로 치환하면, 원래의 방정식에서 다음 식을 얻을 수 있음.

\[z^3+z^2+z+1+\frac{1}{z}+\frac{1}{z^2}+\frac{1}{z^3}=(z+\frac{1}{z})^3+(z+\frac{1}{z})^2-2(z+\frac{1}{z})-1=y^3+y^2-2y-1=0\] 3차 방정식의 근의 공식을 이용하여 방정식 \(y^3+y^2-2y-1=0\)을 풀면, 다음을 얻는다 \[y_1= \frac{1}{3} \left(-1+\frac{7^{2/3}}{\sqrt[3]{\frac{1}{2} \left(1+3 i \sqrt{3}\right)}}+\sqrt[3]{\frac{7}{2} \left(1+3 i \sqrt{3}\right)}\right)(=2\cos\frac{2\pi}{7})\] \[y_2=-\frac{1}{3}-\frac{7^{2/3} \left(1+i \sqrt{3}\right)}{3\ 2^{2/3} \sqrt[3]{1+3 i \sqrt{3}}}+\frac{1}{6} i \sqrt[3]{\frac{7}{2} \left(1+3 i \sqrt{3}\right)} \left(\sqrt{3}+i\right)(=2\cos\frac{4\pi}{7})\] \[y_3=-\frac{1}{3}-\frac{1}{6} \left(1+i \sqrt{3}\right) \sqrt[3]{\frac{7}{2} \left(1+3 i \sqrt{3}\right)}+\frac{i 7^{2/3} \left(\sqrt{3}+i\right)}{3\ 2^{2/3} \sqrt[3]{1+3 i \sqrt{3}}}(=2\cos\frac{6\pi}{7})\] 이제 \(z^2-yz+1=0\)로부터 \(z=\frac{y+\sqrt{y^2-4}}{2}\)

정칠각형의 대각선의 길이

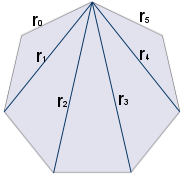
• 한 변의 길이가 1인 정칠각형의 대각선의 길이 \(r_i\)는 \(i=0,1,\cdots,5\)에 대하여 다음과 같이 주어짐 \[r_i=\frac{\sin \frac{(i+1)\pi}{7}}{\sin \frac{\pi}{7}}\] * 이 때 \(r_0=1\), \(r_5=1\)
• 제2종 체비셰프 다항식
• 대각선이 만족시키는 다양한 항등식\[r_hr_k=r_{h-k}+r_{h-k+2}+\cdots+r_{h+k}, 0\leq k\leq h\leq 2\]\[r_i^2=1+r_{i-1}r_{i+1}, 1\leq i \leq 4\]\[r_0r_0=r_0\]\[r_1r_0=r_1\]\[r_1r_1=r_0+r_2\]\[r_2r_0=r_2\]\[r_2r_1=r_1+r_3\]\[r_2r_2=r_0+r_2+r_4\]

• \(r_1\)은 \(x^3-x^2-2x+1=0\) 의 해이다 http://www.wolframalpha.com/input/?i=+%28sin%282pi%2F7%29%2Fsin%28pi%2F7%29%29

(증명)

\(r_1r_1=r_0+r_2\)

\(r_2r_1=r_1+r_3=r_1+r_2\)■

• \(r_2\)은 \(x^3-2x^2-x+1=0\) 의 해이다 http://www.wolframalpha.com/input/?i=+%28sin%283pi%2F7%29%2Fsin%28pi%2F7%29%29

(증명)

\(r_1r_1=r_0+r_2\)

\(r_2r_2=r_0+r_2+r_4=r_0+r_2+r_1\) ■

다이로그 항등식

• 다이로그 항등식 (dilogarithm identities)\[\alpha=\frac{\sec\frac{2\pi}{7}}{2}=0.80194\cdots\]\[\beta=\frac{\sec\frac{\pi}{7}}{2}=0.554958\cdots\]\[\gamma=2\cos\frac{3\pi}{7}=0.445042\cdots\]\[7L(\alpha^2)-7L(\alpha)+L(1)=0\]\[7L(\beta^2)+14L(\beta)-10L(1)=0\]\[7L(\gamma^2)+14L(\gamma)-8L(1)=0\]\[\sum_{i=1}^{5}L\left(\frac{\sin^2\frac{\pi}{7}}{\sin^2\frac{(i+1)\pi}{7}}\right)=\frac{5\pi^2}{14}\]

• 방정식 \(x^3+2x^2-x-1=0\) 의 해 \(\alpha, -\beta, -\gamma^{-1}\)

• 방정식 \(x^3+x^2-2x-1=0\)의 해 \(a,b,c\)

\(a=2\cos\frac{2\pi}{7}=\alpha^{-1}=1.24698\cdots\), \(b=2\cos\frac{4\pi}{7}=-\gamma=-0.445042\cdots\),\(c=2\cos\frac{6\pi}{7}=-\beta^{-1}=-1.80194\cdots\)

• k=3인 경우의 앤드류스-고든 항등식(Andrews-Gordon identity)\[1-x_{1}=x_{1}^{4}x_{2}^{2}\]\[1-x_{2}=x_{1}^{2}x_{2}^{2}\]를 풀면,\[x_{2}=1-\frac{1-x_{1}}{x_{1}^{2}}=\frac{x_{1}^{2}+x_{1}-1}{x_{1}^{2}}\]\[1-x_{1}=(x_{1}^{2}+x_{1}-1)^{2}\] 따라서 \(x_1\)은 \(x (x^3+2 x^2-x-1)=0\)의 해가 된다

역사

• 수학사 연표

관련된 항목들

• 원분체 (cyclotomic field)
• 톨레미의 정리

매스매티카 파일 및 계산 리소스

• http://www.wolframalpha.com/input/?i=regular+heptagon+inscribed+in+a+unit+circle

사전 형태의 자료

• http://ko.wikipedia.org/wiki/칠각형
• http://en.wikipedia.org/wiki/Heptagon

관련논문

• Continued fractions and modular functions
  • W. Duke, Bull. Amer. Math. Soc. 42 (2005), 137-162
• Golden Fields: A Case for the Heptagon
  • Peter Steinbach, Mathematics Magazine Vol. 70, No. 1 (Feb., 1997), pp. 22-31
• A Note on Spence's Logarithmic Transcendent
  • Watson, G. N., Quart. J. Math. Oxford Ser. 8, 39-42, 1937
• ABCDEFG Is a Regular Heptagon in a Circle of Unit Radius; To Prove That AC+AD-AB=√7
  • T. S. Tufton, The Mathematical Gazette Vol. 18, No. 230 (Oct., 1934), pp. 274-275

메타데이터

위키데이터

• ID : Q188866

Spacy 패턴 목록

• [{'LEMMA': 'heptagon'}]
• [{'LEMMA': '7-gon'}]