"감마함수"의 두 판 사이의 차이
Pythagoras0 (토론 | 기여) |
Pythagoras0 (토론 | 기여) (→관련논문) |
||
| 183번째 줄: | 183번째 줄: | ||
* Emil Artin, The Gamma Function | * Emil Artin, The Gamma Function | ||
| + | |||
| + | |||
| + | ==리뷰, 에세이, 강의노트== | ||
| + | * Dutka, Jacques. 1991. “The early history of the factorial function.” <em>Archive for History of Exact Sciences</em> 43 (3): 225-249. doi:[http://dx.doi.org/10.1007/BF00389433 10.1007/BF00389433]. | ||
==관련논문== | ==관련논문== | ||
| + | * Fekih-Ahmed, Lazhar. “On the Power Series Expansion of the Reciprocal Gamma Function.” arXiv:1407.5983 [math], July 22, 2014. http://arxiv.org/abs/1407.5983. | ||
* Paris, R. B. “On the Asymptotic Expansion of $\Gamma(x)$, Lagrange’s Inversion Theorem and the Stirling Coefficients.” arXiv:1405.3423 [math], May 14, 2014. http://arxiv.org/abs/1405.3423. | * Paris, R. B. “On the Asymptotic Expansion of $\Gamma(x)$, Lagrange’s Inversion Theorem and the Stirling Coefficients.” arXiv:1405.3423 [math], May 14, 2014. http://arxiv.org/abs/1405.3423. | ||
| − | * | + | * Chudnovsky, G. “Algebraic Independence of the Values of Elliptic Function at Algebraic Points.” Inventiones Mathematicae 61, no. 3 (October 1, 1980): 267–90. doi:10.1007/BF01390068. |
| − | |||
| − | |||
| − | |||
| − | |||
2014년 7월 23일 (수) 19:02 판
개요
- 팩토리얼 함수의 정의역을 복소수로 확장하는 함수이다.
- 자연수에 대해 팩토리얼과 같은 값을 가지면서 $s > 0$ 일 때 $\log \Gamma(s)$ 가 볼록성을 갖는 유일한 함수이다.
- 다음과 같은 중요한 성질을 갖는다\[\Gamma(s+1) =s\Gamma(s)\]\[\Gamma(1-z) \; \Gamma(z) = {\pi \over \sin{(\pi z)}} \,\!\]\[\Gamma(z) \; \Gamma\left(z + \frac{1}{m}\right) \; \Gamma\left(z + \frac{2}{m}\right) \cdots \Gamma\left(z + \frac{m-1}{m}\right) = (2 \pi)^{(m-1)/2} \; m^{1/2 - mz} \; \Gamma(mz)\]
- 대수다양체의 periods 를 표현하는데 등장하며, \(s\)가 유리수일때의 감마함수의 값이 초월수인지, 그리고 그 값들 사이의 대수적 관계에 대한 문제는 중요 미해결 문제
정의
- 실수부가 \(\Re s>0\)인 복소수 \(s>0\)에 대하여 다음과 같이 정의\[\Gamma(s) = \int_0^\infty e^{-t} t^{s} \frac{dt}{t}\]
- \(\Gamma(s+1) =s\Gamma(s)\)
- 자연수 \(n\)에 대하여 \(\Gamma(n)=(n-1)!\)
- 가우스의 정의\[\Gamma(z) = \lim_{n \to \infty} \frac{n! \; n^z}{z \; (z+1)\cdots(z+n)} \]
해석적확장
- 해석적확장(analytic continuation)
- \(\Gamma(s+1) =s\Gamma(s)\)를 이용하여, 복소평면전체에서 정의된 meromorphic 함수로 이해가능
- \(s=0,-1,-2\cdots\)에서 폴(pole)을 가진다
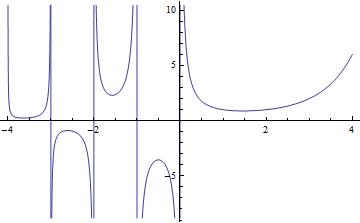
함수의 그래프
- \(-4<s<4\)의 범위에서 다음과 같은 그래프를 가짐
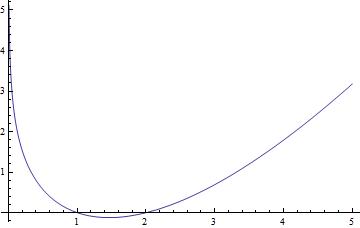
- \(s>0\)일 때, \(\ln \Gamma(s)\)의 그래프
무한곱표현
- 바이어슈트라스 무한곱
\[\Gamma(z) = \frac{e^{-\gamma z}}{z} \prod_{n=1}^\infty \left(1 + \frac{z}{n}\right)^{-1} e^{z/n}\]
반사공식
- \(\Gamma(1-z) \; \Gamma(z) = {\pi \over \sin{(\pi z)}} \,\!\)
(증명)
삼각함수의 무한곱 표현 \[\sin{\pi x} = \pi x \prod _{n=1}^{\infty } \left(1-\frac{x^2}{n^2}\right)\] 과 \[\Gamma(z) = \frac{e^{-\gamma z}}{z} \prod_{n=1}^\infty \left(1 + \frac{z}{n}\right)^{-1} e^{z/n}\] 를 써서 증명된다. ■
- 다음 계산을 얻는다
\[\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}\]
- 일반적으로 \[\Gamma(n+\frac{1}{2})=(\frac{1}{2})_n\sqrt{\pi}\]
(증명) \[\Gamma(n+\frac{1}{2})=\Gamma(\frac{2n+1}{2})=(\frac{2n-1}{2})\Gamma(\frac{2n-1}{2})=(\frac{2n-1}{2})(\frac{2n-3}{2})\Gamma(\frac{2n-3}{2})=(\frac{2n-1}{2})\cdots(\frac{1}{2})\Gamma(\frac{1}{2})=\frac{1}{2}\cdot\frac{3}{2}\cdot\frac{2n-1}{2}\sqrt{\pi}=(\frac{1}{2})_n\sqrt{\pi}\]■
곱셈공식
- 이항
\[\Gamma(z) \; \Gamma\left(z + \frac{1}{2}\right) = 2^{\frac{1}{2}-2z} \; \sqrt{2\pi} \; \Gamma(2z) \,\!\]\[2^{2z}\Gamma(z) \; \Gamma\left(z + \frac{1}{2}\right) = 2\sqrt{\pi}\;\Gamma(2z)\]
- 일반화\[\Gamma(z) \; \Gamma\left(z + \frac{1}{m}\right) \; \Gamma\left(z + \frac{2}{m}\right) \cdots \Gamma\left(z + \frac{m-1}{m}\right) = (2 \pi)^{(m-1)/2} \; m^{1/2 - mz} \; \Gamma(mz)\]
적분표현
- Binet's second expression
- \(\operatorname{Re} z > 0 \) 일 때,
\[\log \Gamma(z)=(z-\frac{1}{2})\log z -z+\frac{1}{2}\log 2\pi+ 2\int_0^{\infty}\frac{\tan^{-1}(t/z)}{e^{2\pi t} -1}dt\]
Hurwitz 제타함수와의 관계
- 적당한 상수 R이 존재하여 \(\Gamma(a)=R{e^{\zeta'(0,a)}}\)
- 후르비츠 제타함수(Hurwitz zeta function) 참조
쿰머의 푸리에 급수
- 로그감마 함수의 푸리에 급수
\[\begin{eqnarray}\log\Gamma(x)=\log\sqrt{2\pi}-\frac{1}{2}\log(2\sin\pi x)+\frac{1}{2}(\gamma+2\log\sqrt{2\pi})(1-2x)+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{\log k}{k}\sin 2\pi kx \nonumber \\ =(\frac{1}{2}-x)(\gamma+\log 2)+(1-x)\log \pi -\frac{1}{2}\log(\sin\pi x)+\frac{1}{\pi}\sum_{k=1}^{\infty}\frac{\log k}{k}\sin 2\pi kx \nonumber \end{eqnarray} \]
테일러 급수
- 로그감마 함수의 테일러 급수\[\log\Gamma(1+x) =-\gamma x+\sum_{k=2}^{\infty}(-1)^k \frac{\zeta(k)}{k}x^k\]
다이감마 함수
- 감마함수의 로그미분으로 정의
\[\psi(x) =\frac{d}{dx} \ln{\Gamma(x)}= \frac{\Gamma'(x)}{\Gamma(x)}\]
- 자세한 사실은 다이감마 함수(digamma function) 항목 참조.
오일러 베타적분
- 오일러 베타적분 항목 참조
\[B(x,y)=\dfrac{\Gamma(x)\,\Gamma(y)}{\Gamma(x+y)}\]
감마함수와 초월수
- 감마함수의 유리수에서의 값이 초월수인지의 문제.
- 다음 경우가 초월수 임이 알려져 있다
\[\Gamma(\frac{1}{3}),\Gamma(\frac{2}{3}),\Gamma(\frac{1}{4}),\Gamma(\frac{3}{4}),\Gamma(\frac{1}{6}),\Gamma(\frac{5}{6})\]
- 미해결 문제. 다음은 초월수인가?
\[\Gamma(\frac{1}{5})\]
- 무리수와 초월수 항목 참조
메모
역사
- 1811년 르장드르가 팩토리얼의 확장을 나타내기 위하여 $\Gamma$ 기호를 도입
- The birth of the real factorial function
- http://mathoverflow.net/questions/9746/who-invented-the-gamma-function
- http://mathoverflow.net/questions/156495/why-does-the-gamma-function-use-the-symbol-gamma
관련된 항목들
하위페이지
- 감마곱 (Gamma Products)
- 다이감마 함수(digamma function)
- 더블감마함수와 Barnes G-함수
- 로그감마 함수
- 멀티 감마함수(multiple gamma function)
- 트리감마 함수(trigamma function)
- 폴리감마함수(polygamma functions)
매스매티카 파일 및 계산 리소스
- https://docs.google.com/leaf?id=0B8XXo8Tve1cxZmM5YWZjMzAtZmVjNS00OWUxLWJhZGUtMzMwN2Q4YmI5ZTIz&sort=name&layout=list&num=50
- http://functions.wolfram.com/
- NIST Digital Library of Mathematical Functions
사전형태의 자료
- http://ko.wikipedia.org/wiki/감마함수
- http://en.wikipedia.org/wiki/gamma_function
- http://en.wikipedia.org/wiki/Particular_values_of_the_Gamma_function
- http://en.wikipedia.org/wiki/Bohr–Mollerup_theorem
- http://mathworld.wolfram.com/BinetsLogGammaFormulas.html
관련도서
- Emil Artin, The Gamma Function
리뷰, 에세이, 강의노트
- Dutka, Jacques. 1991. “The early history of the factorial function.” Archive for History of Exact Sciences 43 (3): 225-249. doi:10.1007/BF00389433.
관련논문
- Fekih-Ahmed, Lazhar. “On the Power Series Expansion of the Reciprocal Gamma Function.” arXiv:1407.5983 [math], July 22, 2014. http://arxiv.org/abs/1407.5983.
- Paris, R. B. “On the Asymptotic Expansion of $\Gamma(x)$, Lagrange’s Inversion Theorem and the Stirling Coefficients.” arXiv:1405.3423 [math], May 14, 2014. http://arxiv.org/abs/1405.3423.
- Chudnovsky, G. “Algebraic Independence of the Values of Elliptic Function at Algebraic Points.” Inventiones Mathematicae 61, no. 3 (October 1, 1980): 267–90. doi:10.1007/BF01390068.