"대문"의 두 판 사이의 차이
둘러보기로 가기
검색하러 가기
Pythagoras0 (토론 | 기여) 잔글 (MediaWiki default(토론)의 편집을 Pythagoras0의 마지막 버전으로 되돌림) |
Pythagoras0 (토론 | 기여) (→머신 러닝) |
||
| (같은 사용자의 중간 판 16개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | == | + | ==모든 문서== |
| + | * [[특수기능:모든문서|현재 전체 문서 목록]] | ||
* [[기존 스프링노트에서의 전체 문서 목록]] | * [[기존 스프링노트에서의 전체 문서 목록]] | ||
| − | * [ | + | * [http://twitter.com/bot_math 트위터 수학노트봇 계정] |
| + | |||
== 왼쪽상단의 이미지 설명== | == 왼쪽상단의 이미지 설명== | ||
| − | * | + | * 노르웨이의 수학자 [[닐스 헨릭 아벨(1802 – 1829)]]을 기념하기 위한 우표 |
| − | * | + | * 일반적인 오차이상의 방정식의 해는 사칙연산과 근호를 사용하여 나타낼수 없음을 최초로 증명 |
** [[5차방정식과 근의 공식]] | ** [[5차방정식과 근의 공식]] | ||
** [[5차방정식의 근의 공식과 아벨의 증명]] | ** [[5차방정식의 근의 공식과 아벨의 증명]] | ||
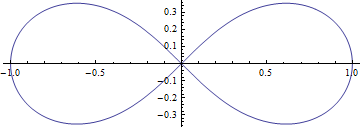
| − | * | + | * 우표 왼쪽의 무한대 모양은 아벨이 [[타원적분]]을 연구하는데 길잡이 역할을 한 렘니스케이트 곡선 |
** [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분|렘니스케이트(lemniscate) 곡선과 타원적분]] 항목 참조 | ** [[렘니스케이트(lemniscate) 곡선의 길이와 타원적분|렘니스케이트(lemniscate) 곡선과 타원적분]] 항목 참조 | ||
[[파일:렘니스케이트(lemniscate) 곡선의 길이와 타원적분1.png|center]] | [[파일:렘니스케이트(lemniscate) 곡선의 길이와 타원적분1.png|center]] | ||
| − | + | * [[타원적분론 입문]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * [[ | ||
| − | |||
| − | |||
| − | |||
==고등수학 입문== | ==고등수학 입문== | ||
| 28번째 줄: | 20번째 줄: | ||
* [[고교생도 이해할 수 있는 군론 입문]] | * [[고교생도 이해할 수 있는 군론 입문]] | ||
* [[분수와 순환소수]] | * [[분수와 순환소수]] | ||
| + | * [[미적분학 입문]] | ||
* [[비유클리드 기하학]] | * [[비유클리드 기하학]] | ||
** [[구면기하학]] | ** [[구면기하학]] | ||
** [[쌍곡기하학]] | ** [[쌍곡기하학]] | ||
| − | |||
| − | == | + | ==기계 학습== |
| − | + | * [[기계 학습]] | |
| − | + | * [[마르코프 체인]]을 이용한 [https://markov.mathnt.net 인공저능 p봇 베타] | |
| − | * [[ | ||
| − | * [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==재미있는 수학의 주제들== | ==재미있는 수학의 주제들== | ||
| − | + | * [[원근법과 수학]] | |
| + | [[파일:4777527-parallel (2).jpg|600px]] | ||
* [[체커보드의 원근법]] | * [[체커보드의 원근법]] | ||
[[파일:floor.gif]] | [[파일:floor.gif]] | ||
| 56번째 줄: | 40번째 줄: | ||
** [[파이가 아니라 2파이다?]] | ** [[파이가 아니라 2파이다?]] | ||
** [[지식채널e '끝없는 3.14']] | ** [[지식채널e '끝없는 3.14']] | ||
| − | |||
** [[라마누잔과 파이]] | ** [[라마누잔과 파이]] | ||
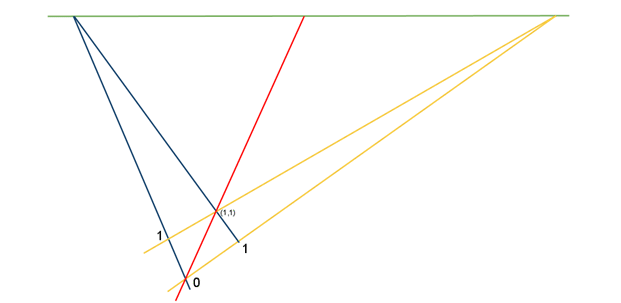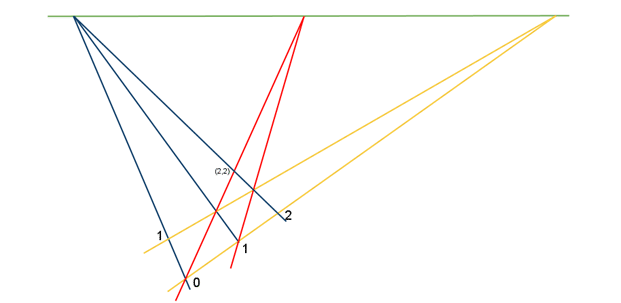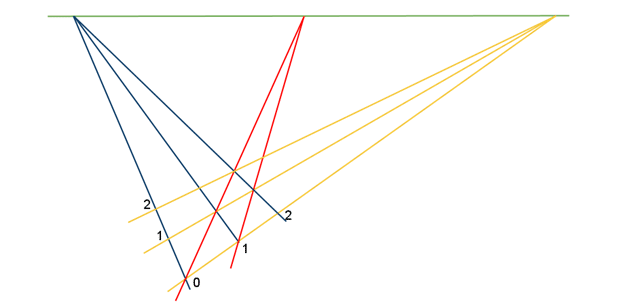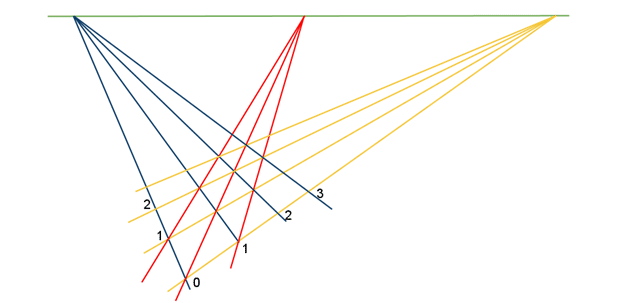
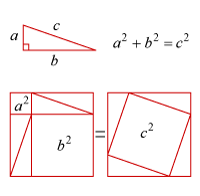
* [[피타고라스의 정리]] | * [[피타고라스의 정리]] | ||
** 그림증명 | ** 그림증명 | ||
| − | [[파일: | + | [[파일:1978936-pythagorean theorem.gif]] |
| + | * [[EBS '다큐프라임' 3부작 피타고라스 정리의 비밀']] | ||
| + | |||
| + | |||
| + | ==생활 속의 수학== | ||
| − | * [[ | + | * [[A4 종이와 루트2|A4와 루트2]] |
| + | * [[ISBN과 주민등록번호 |ISBN과 주민등록번호]] | ||
| + | * [[달력의 수학]] | ||
| + | * [[수학과 음악]] | ||
| + | * [[수학과 지도학|지도와 수학]] | ||
| + | * [[축구공의 수학]] | ||
| + | * [[타원과 인간]] | ||
| + | * [[타자의 타율과 연분수]] | ||
2020년 12월 22일 (화) 20:55 기준 최신판
모든 문서
왼쪽상단의 이미지 설명
- 노르웨이의 수학자 닐스 헨릭 아벨(1802 – 1829)을 기념하기 위한 우표
- 일반적인 오차이상의 방정식의 해는 사칙연산과 근호를 사용하여 나타낼수 없음을 최초로 증명
- 우표 왼쪽의 무한대 모양은 아벨이 타원적분을 연구하는데 길잡이 역할을 한 렘니스케이트 곡선
_%EA%B3%A1%EC%84%A0%EC%9D%98_%EA%B8%B8%EC%9D%B4%EC%99%80_%ED%83%80%EC%9B%90%EC%A0%81%EB%B6%841.png)
고등수학 입문
기계 학습
- 기계 학습
- 마르코프 체인을 이용한 인공저능 p봇 베타
재미있는 수학의 주제들
.jpg)
- 피타고라스의 정리
- 그림증명
